|
|
 |
|
This page was automatically generated by make_maps_and_html.py on 2010-12-20 10:22
Bayesian analysis of UK place-names - revised 2008 version
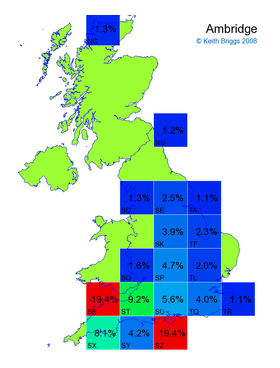
or, where is Ambridge, anyway?
The idea
This is an idea inspired by these initially disconnected thoughts:
- Drawing maps of the distribution of place-name types is an old game -
see e.g. Smith's English place-name elements or Watts' Cambridge dictionary of English place-names (pages li-lxii). I have even automated the process myself with my maps here. But this process is deterministic.
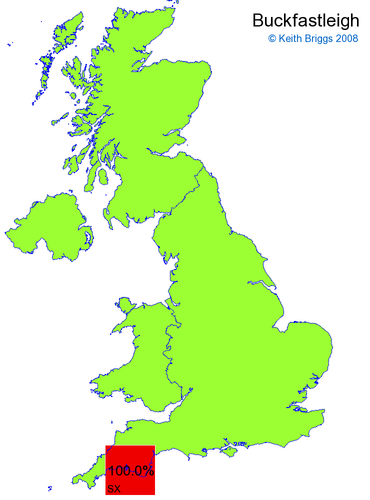
- By contrast, we all have a feeling about different place-name types in the various regions. For example, Buckfastleigh could only be in Devon, Giggleswick in Yorkshire, and Flegg in Norfolk.
But is there any science in this? Could we capture feelings such as these
in a mathematical model? If we could, it would have to be a probabilistic
model.
- In the last few years big advances in Bayesian text classification (both
in theory and in practice) have been stimulated by the requirements of spam
filtering. Can we exploit these advances?
- Made-up place-names in novels and films always sound wrong, even though they are made up of the right elements. Why is this?
The method
So this is what I have done:
- I built Bayesian models for each square in the National Grid, using all
village, town, farm, river etc. names in each square from a gazetteer of 251307 names in total (my previous version used only 29326 names).
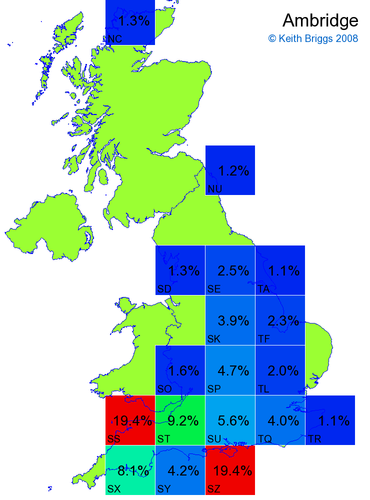
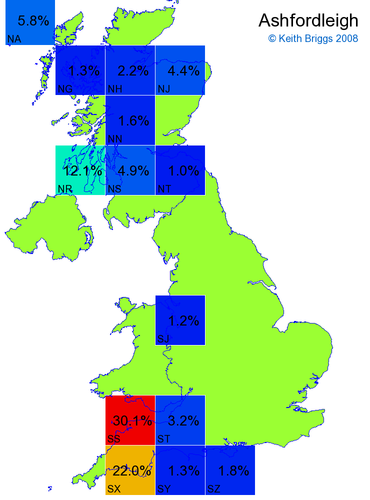
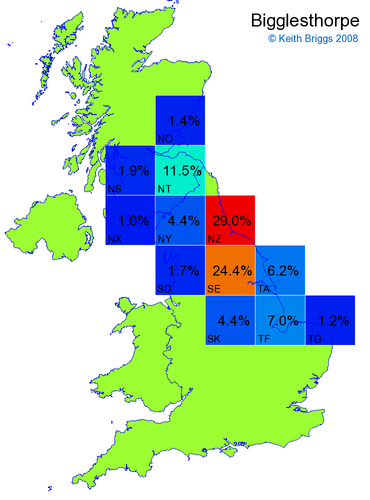
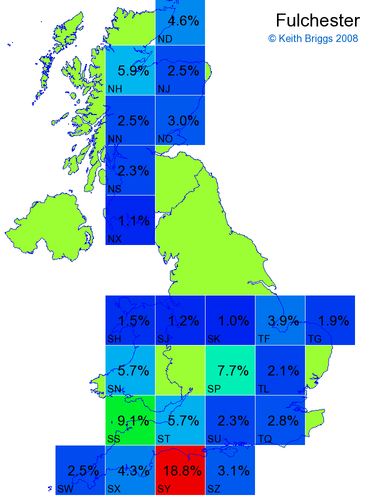
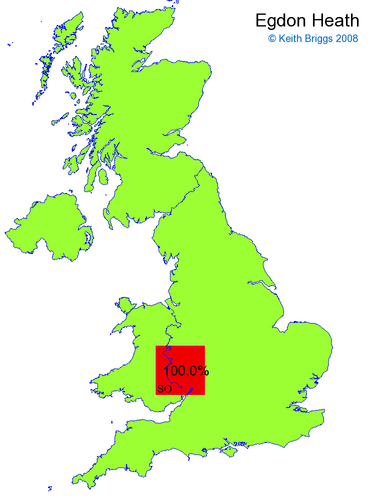
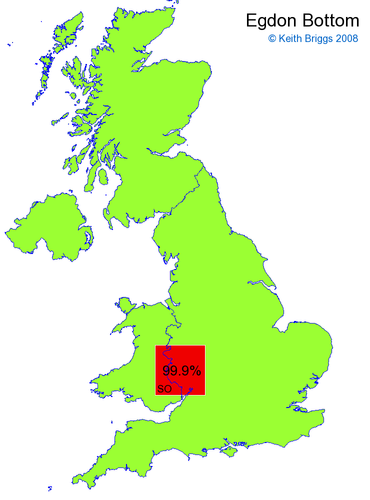
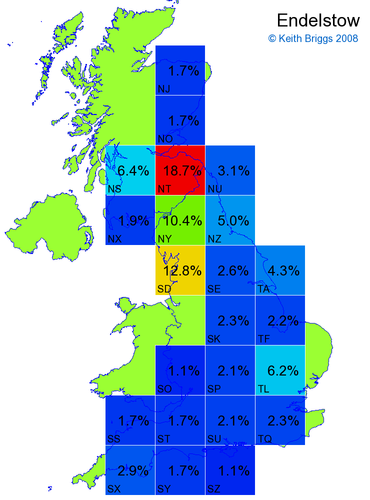
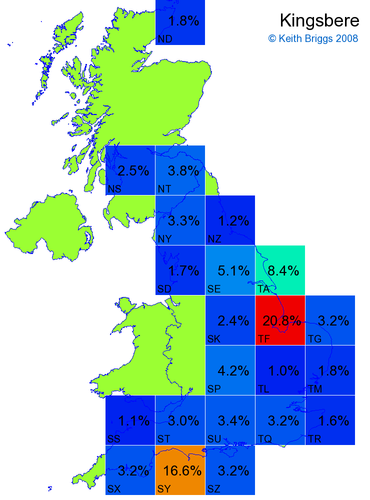
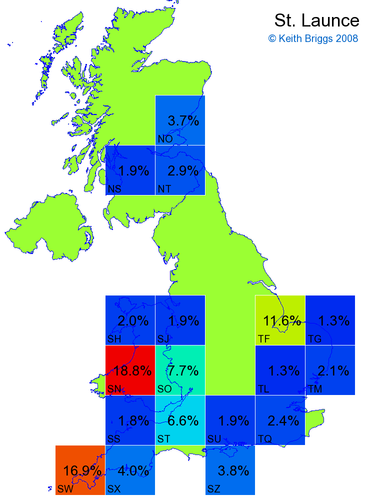
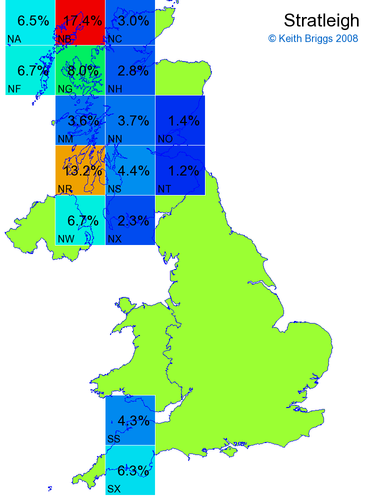
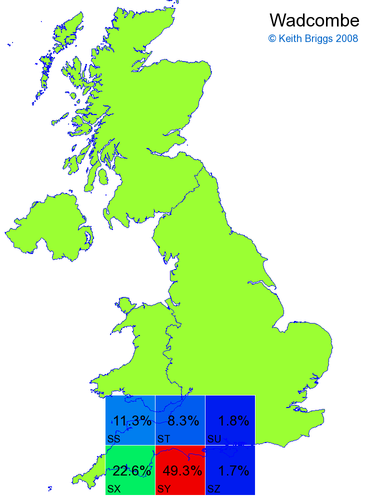
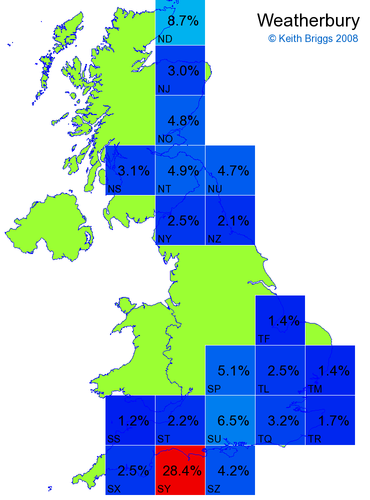
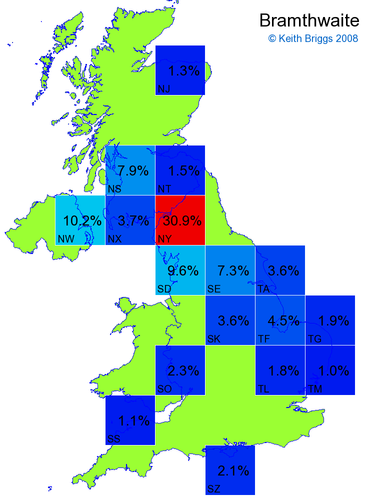
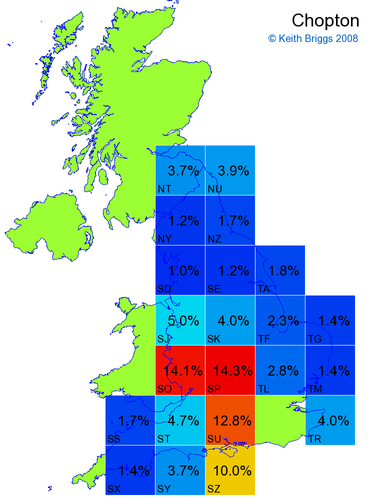
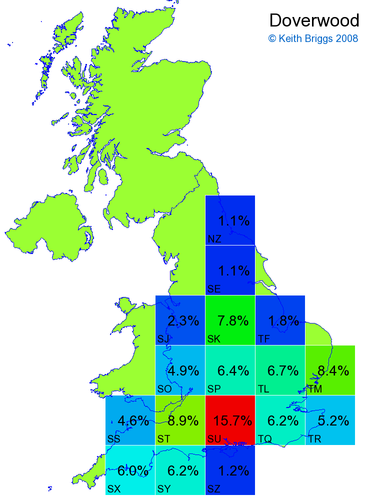
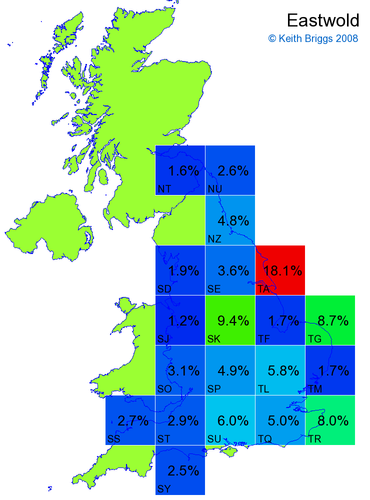
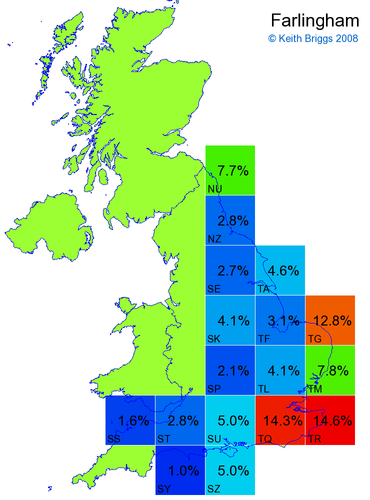
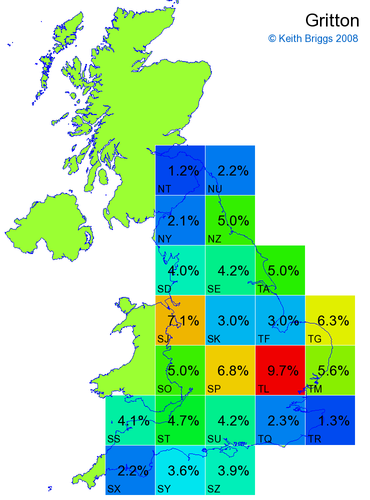
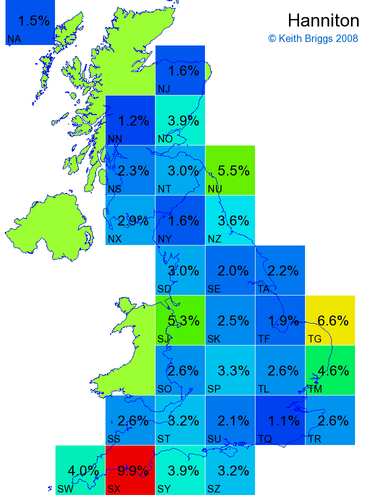
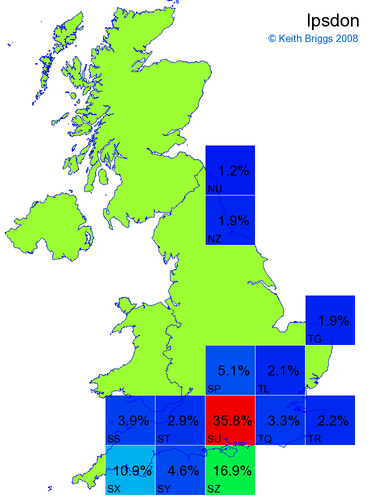
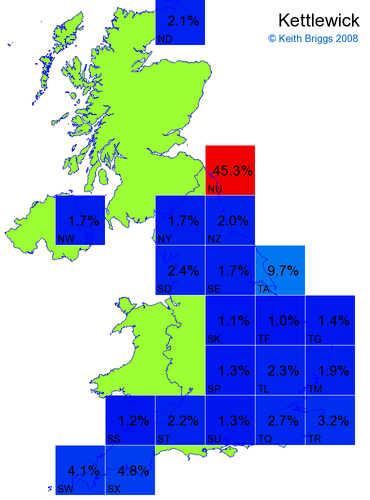
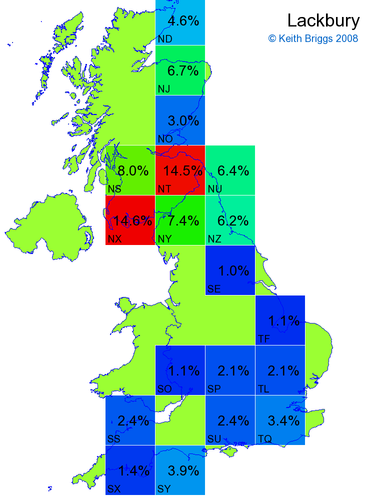
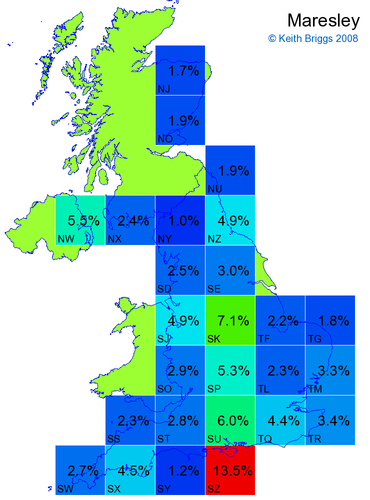
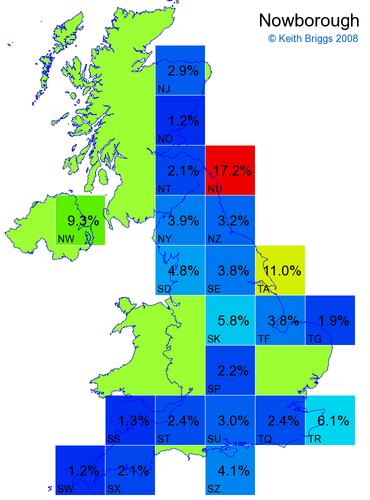
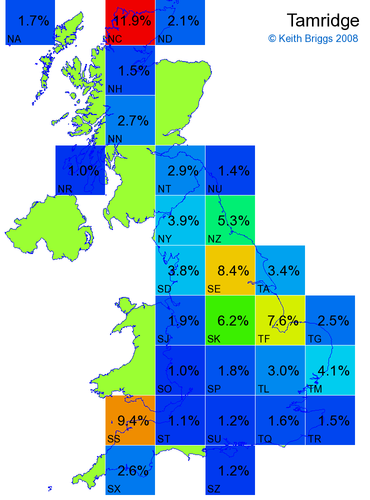
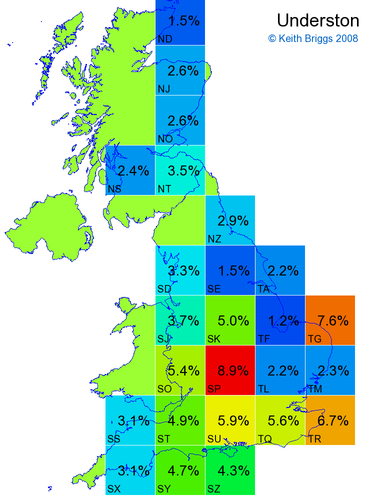
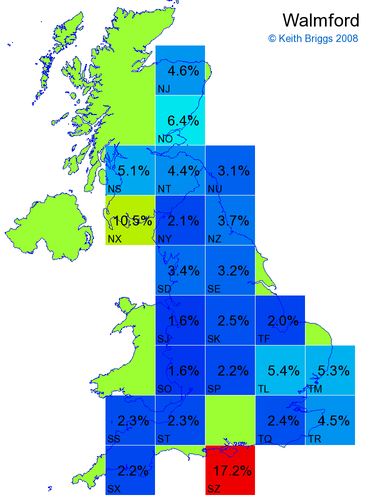
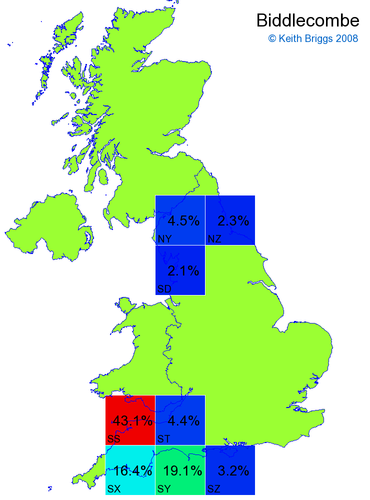
- For each non-existent name below, I computed the posterior probability for it to be in each square according to the model. Some of my made-up names now actually exist (Chopton, Hanton, Marsley), so I have made up slightly different new names in these cases (Chipton, Hanniton, Maresley).
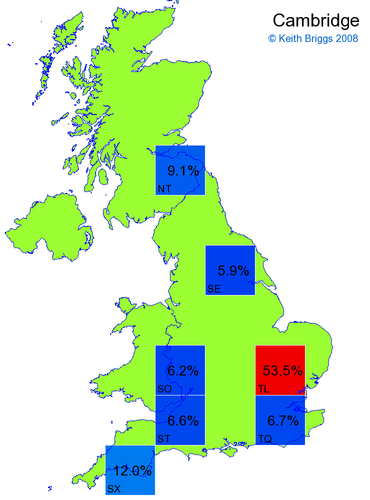
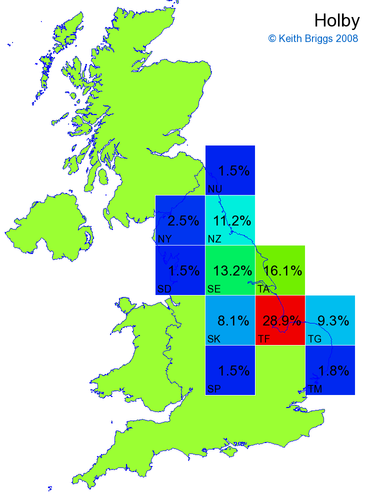
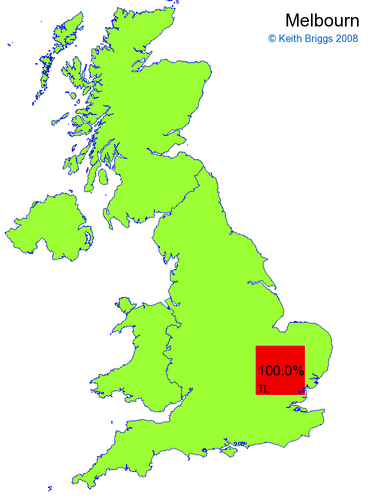
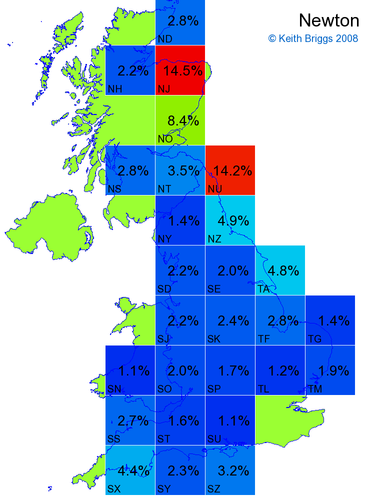
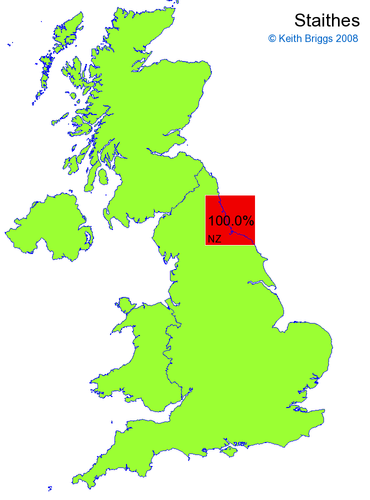
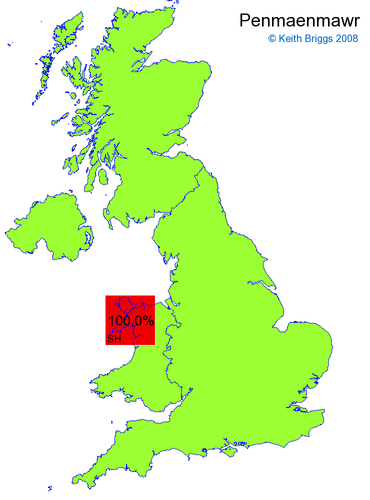
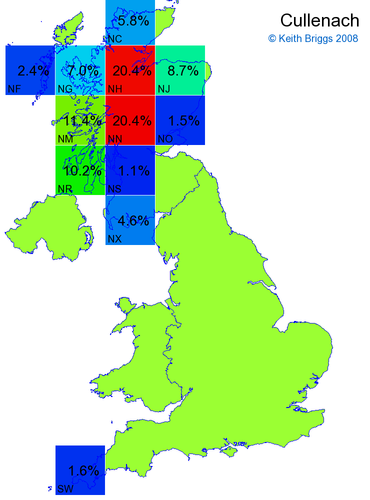
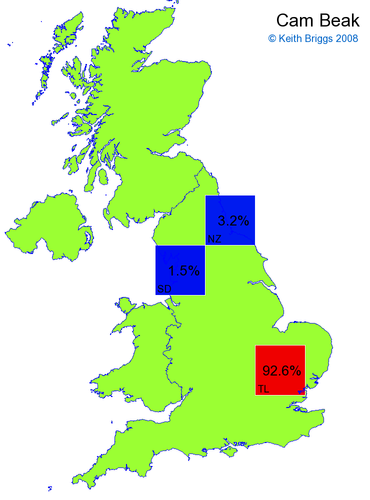
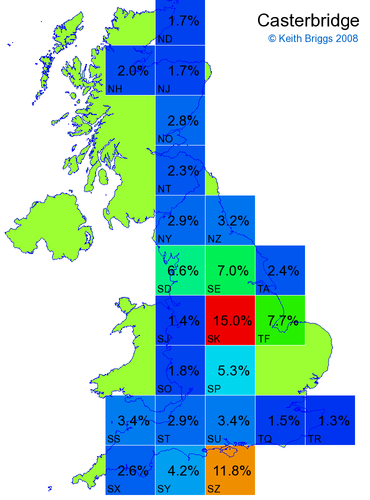
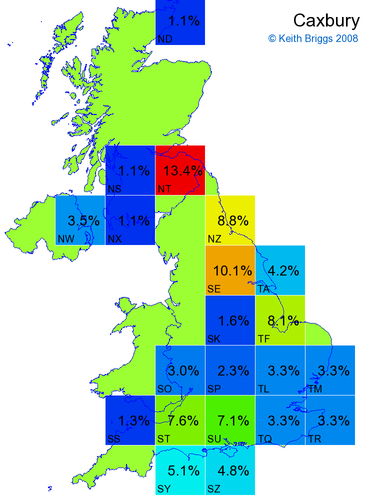
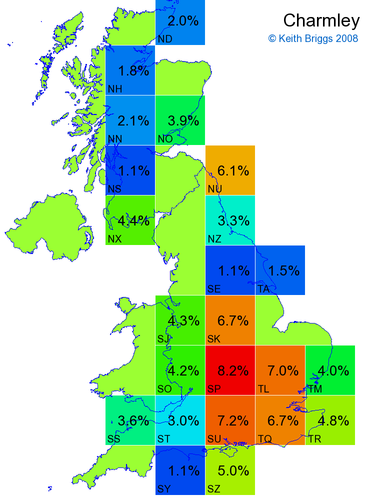
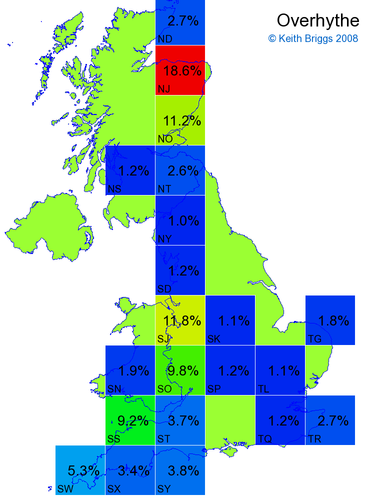
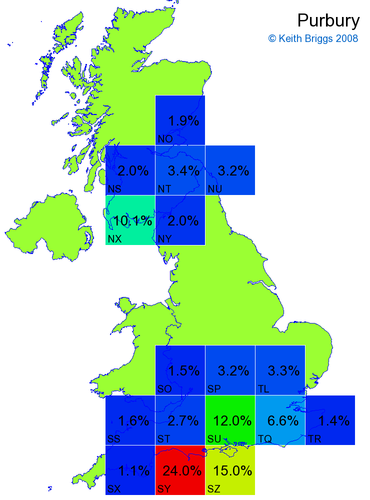
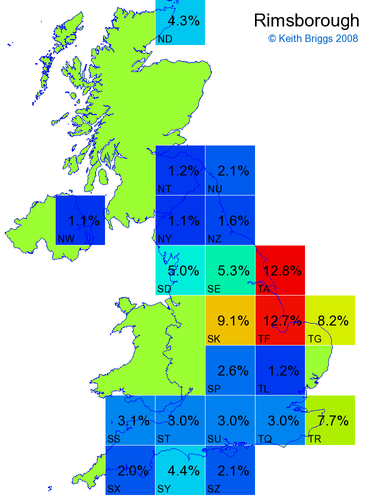
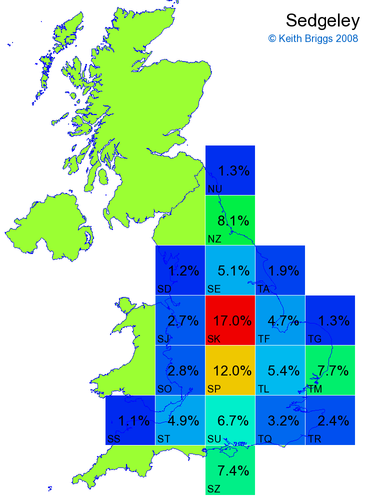
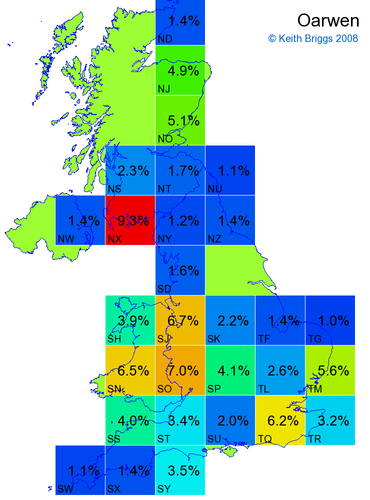
- If the probability was above 1%, I coloured the square with an approximately spectral colour proportional to the probability. Dark blue indicates a very small probability, and bright red the maximum probability, with the levels in between being light blue, green, yellow, and orange, except that in the maps, the largest probability is scaled to 1 to determine the colour. See the key lower down on this page.
- Thus, the reddest square would be the likeliest place for the non-existent name to be located, if it really existed.
- In essence, I am doing text classification with 49 categories, rather than the three (spam, possible spam, legitimate email) as is done in spam filtering.
Some initial checks
Just to check that the whole idea is sensible, we'll do some real names first. Note that the model does not know the location of any place-name.
But if this idea is at all reasonable, it should get real English place-names in roughly the right places, and it should be able to locate Welsh and Gaelic names. Here are some checks of this type. (Note that there really is a Cambridge in Gloucestershire.)
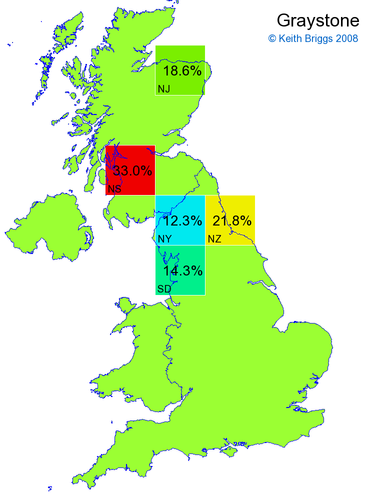
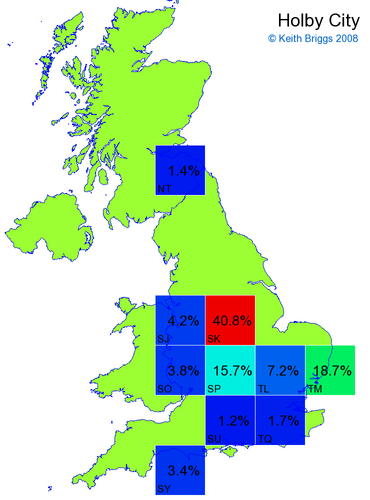
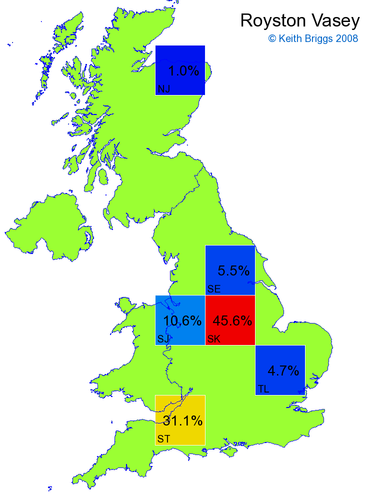
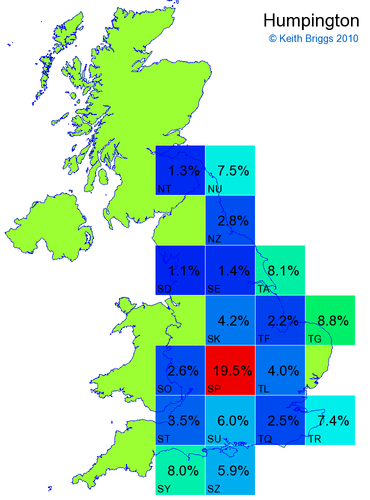
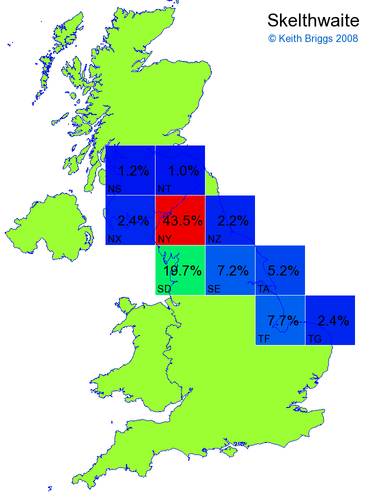
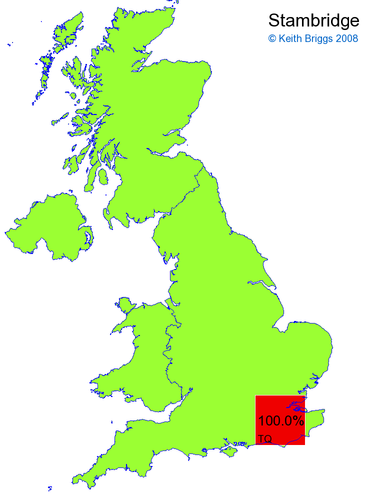
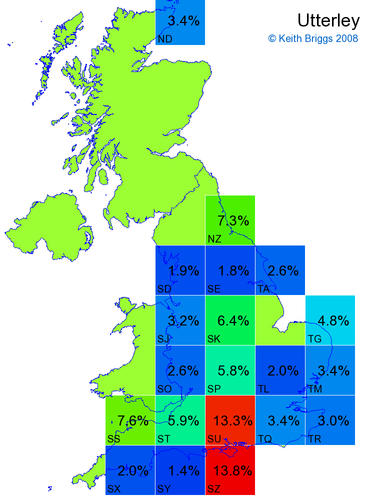
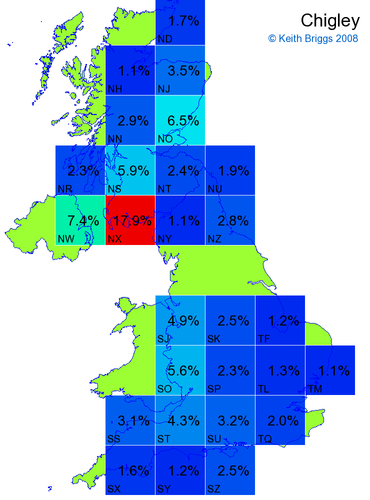
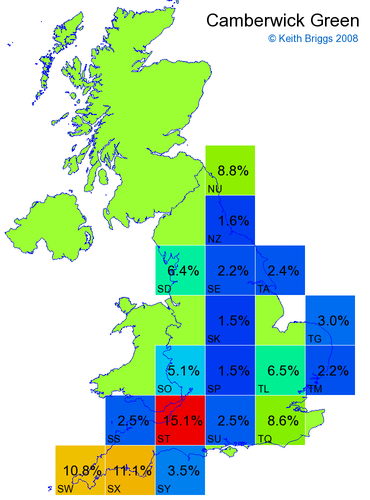
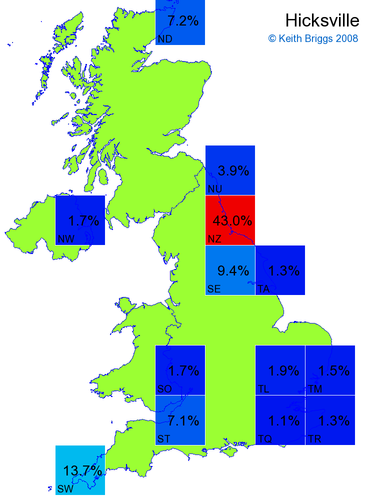
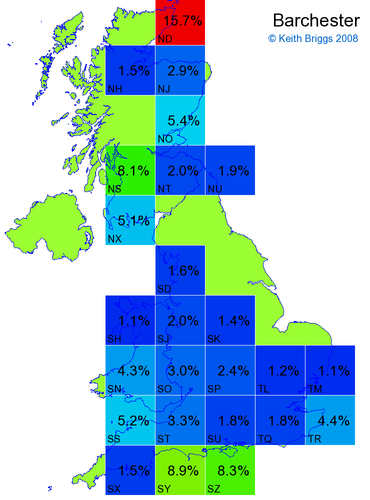
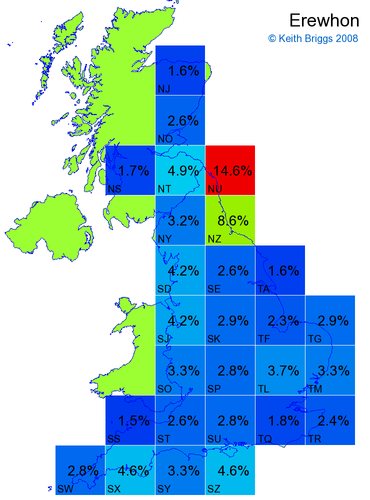
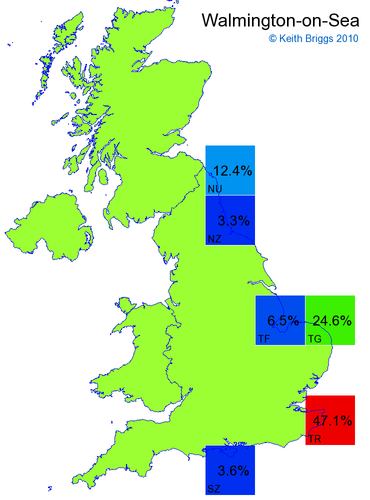
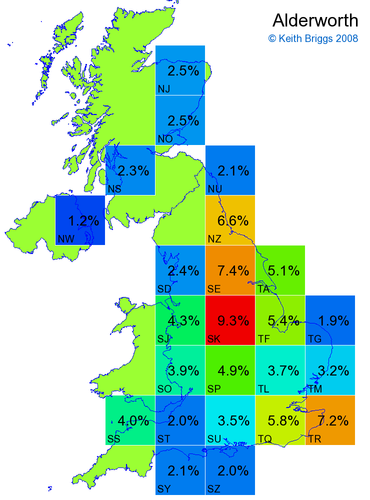
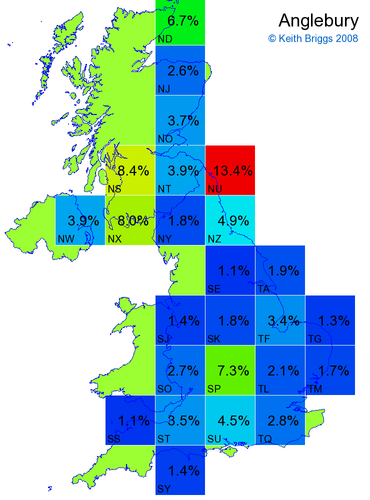
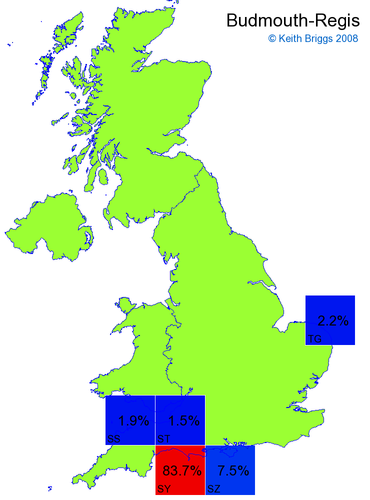
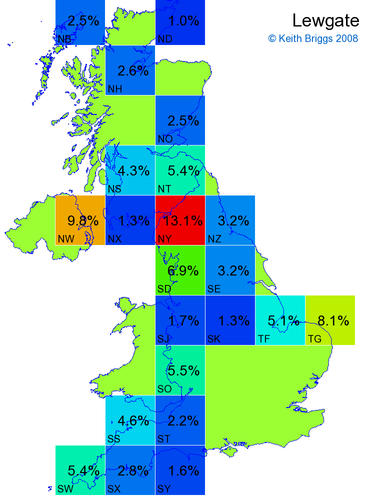
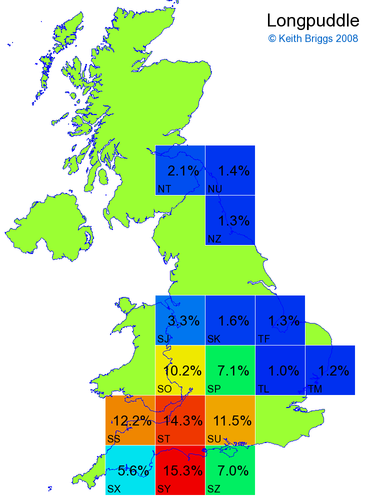
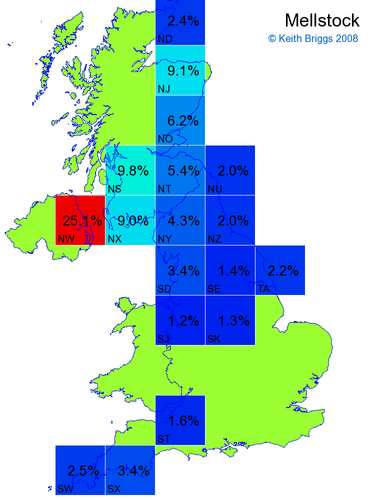
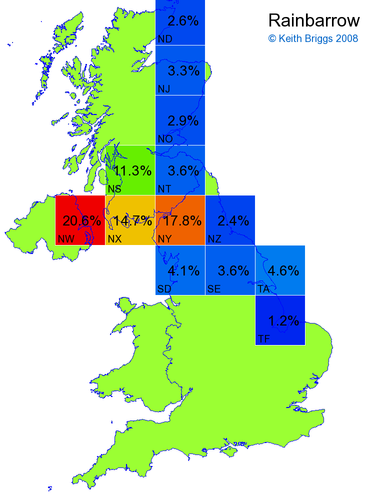
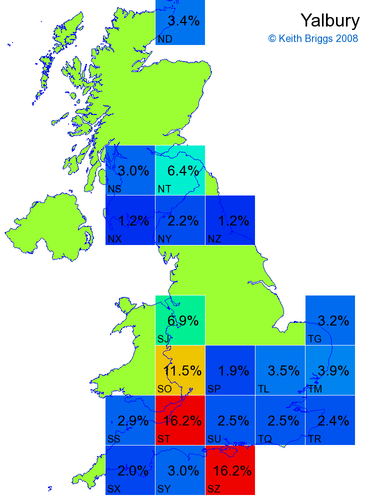
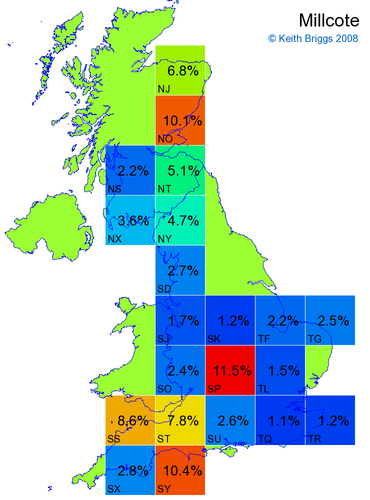
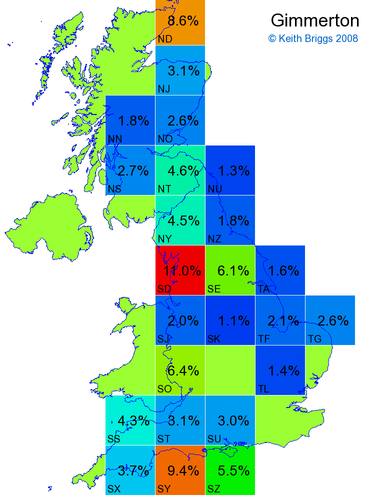
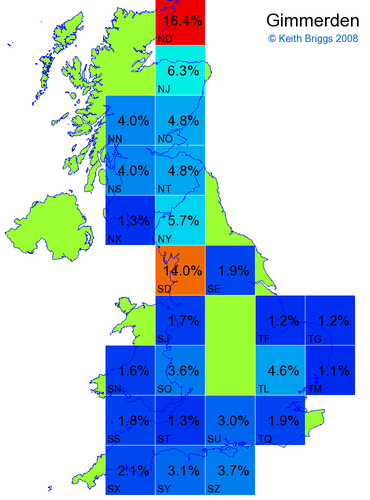
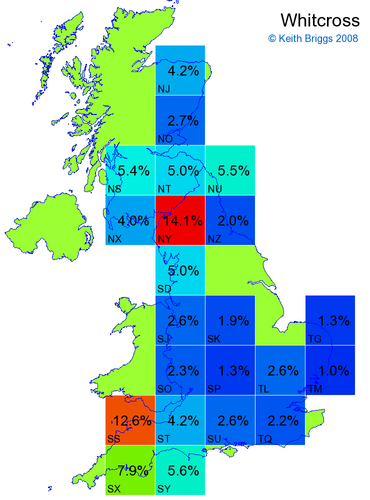
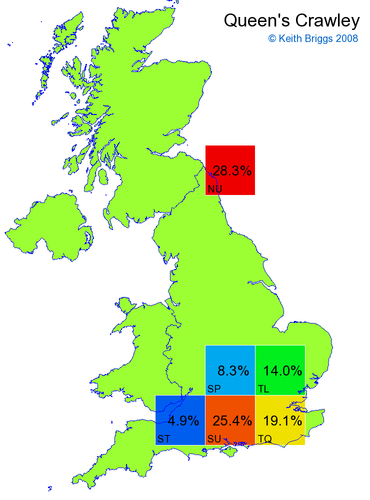
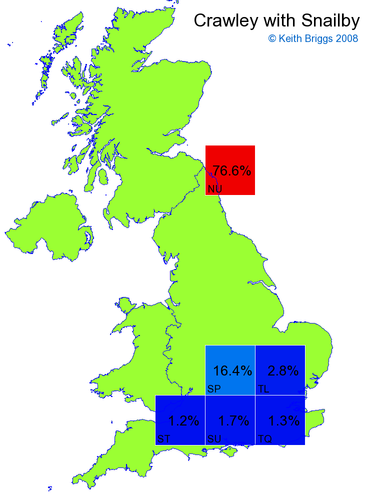
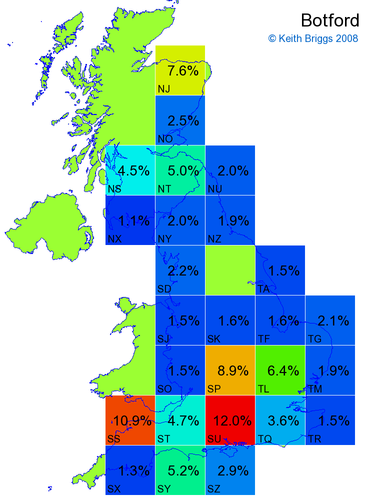
Made-up names from radio, television, films, and comics
Here, the lower the peak probability, the less the name resembles a real name.
Names made up by Hardy
Names made up by the Brontës
Made-up names from other novels
Names made up by me
Technical details
This is the colour coding used in the maps:

For computing the Bayesian models, I used the dbacl software by Laird Breyer.
The next table gives the number of names per square used to build the Bayesian models, and the easting, northing, latitude and longitude of its bottom left-hand corner.
| square | number | easting | northing | latitude | longitude |
|---|
| NA |
143 |
0 |
900 |
57.810 |
-8.739 |
| NB |
2569 |
100 |
900 |
57.889 |
-7.063 |
| NC |
3426 |
200 |
900 |
57.945 |
-5.380 |
| ND |
1723 |
300 |
900 |
57.978 |
-3.691 |
| NF |
1724 |
0 |
800 |
56.918 |
-8.577 |
| NG |
4732 |
100 |
800 |
56.994 |
-6.941 |
| NH |
6243 |
200 |
800 |
57.048 |
-5.298 |
| NJ |
8340 |
300 |
800 |
57.080 |
-3.650 |
| NM |
5303 |
100 |
700 |
56.098 |
-6.825 |
| NN |
6639 |
200 |
700 |
56.151 |
-5.220 |
| NO |
7906 |
300 |
700 |
56.182 |
-3.611 |
| NR |
3795 |
100 |
600 |
55.203 |
-6.716 |
| NS |
9727 |
200 |
600 |
55.253 |
-5.147 |
| NT |
8673 |
300 |
600 |
55.284 |
-3.575 |
| NU |
1129 |
400 |
600 |
55.294 |
-2.000 |
| NW |
91 |
100 |
500 |
54.307 |
-6.613 |
| NX |
5954 |
200 |
500 |
54.356 |
-5.078 |
| NY |
11883 |
300 |
500 |
54.386 |
-3.540 |
| NZ |
5803 |
400 |
500 |
54.395 |
-2.000 |
| SD |
9264 |
300 |
400 |
53.487 |
-3.507 |
| SE |
11233 |
400 |
400 |
53.496 |
-2.000 |
| SH |
6325 |
200 |
300 |
52.561 |
-4.951 |
| SJ |
12063 |
300 |
300 |
52.588 |
-3.476 |
| SK |
9911 |
400 |
300 |
52.597 |
-2.000 |
| SN |
8551 |
200 |
200 |
51.663 |
-4.892 |
| SO |
11753 |
300 |
200 |
51.689 |
-3.447 |
| SP |
9163 |
400 |
200 |
51.698 |
-2.000 |
| SS |
6278 |
200 |
100 |
50.764 |
-4.836 |
| ST |
10496 |
300 |
100 |
50.790 |
-3.419 |
| SU |
10435 |
400 |
100 |
50.799 |
-2.000 |
| SW |
2960 |
100 |
0 |
49.824 |
-6.172 |
| SX |
6787 |
200 |
0 |
49.866 |
-4.783 |
| SY |
2052 |
300 |
0 |
49.891 |
-3.392 |
| SZ |
1146 |
400 |
0 |
49.900 |
-2.000 |
| TA |
1847 |
500 |
400 |
53.487 |
-0.493 |
| TF |
5051 |
500 |
300 |
52.588 |
-0.524 |
| TG |
1642 |
600 |
300 |
52.561 |
0.951 |
| TL |
9503 |
500 |
200 |
51.689 |
-0.553 |
| TM |
4453 |
600 |
200 |
51.663 |
0.892 |
| TQ |
10194 |
500 |
100 |
50.790 |
-0.581 |
| TR |
1550 |
600 |
100 |
50.764 |
0.836 |
This website uses no cookies. This page was last modified 2024-01-21 10:57
by  . .
|
|