Superabundant and colossally abundant numbers

My purpose here is to show some new numerical data concerning these numbers. For more details see my paper Abundant numbers and the Riemann hypothesis, Experimental Mathematics 15, 251-6 (2006).

Definitions:

• σ(n) is the sum of divisors of the positive integer n
• n is perfect if σ(n)=2n
• n is superabundant if σ(m)/m < σ(n)/n for all m<n
• n is colossally abundant if there exists ε>0 such that σ(n)/n^1+ε ≥ σ(k)/k^1+ε for all k>1

data

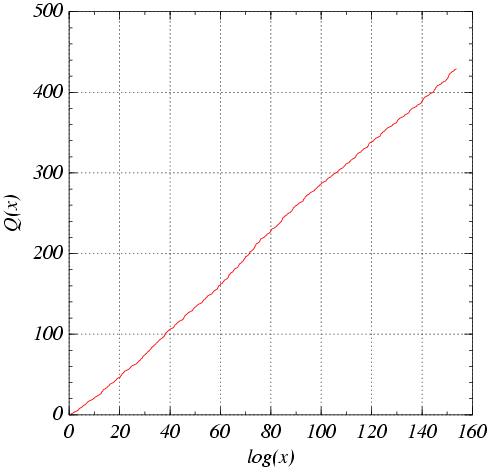
Cumulative number of superabundant numbers:

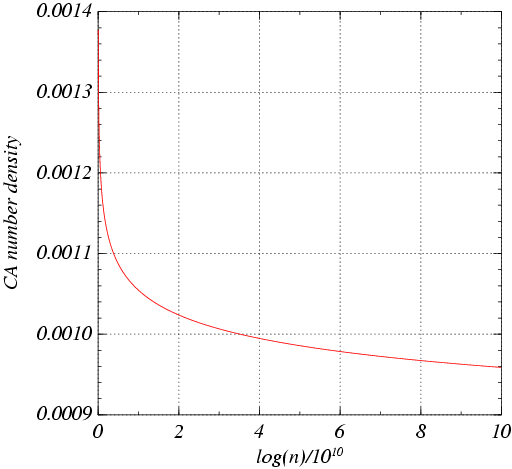
Density of colossally abundant numbers:

references