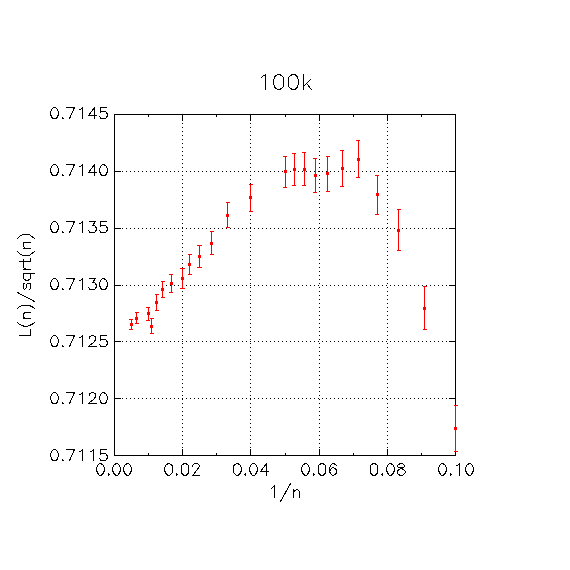
The travelling salesman problem for randomly distributed nodes

Suppose n nodes are uniformly distributed (iid) on a unit 2-torus. I use a torus to avoid edge effects. What is the expected path length L(n) of the optimum travelling salesman problem (TSP) tour in Euclidean norm?

It is known that lim_n→∞ L(n)/sqrt(n) exists and is about 0.7120 (see [1]). Here is my data, which is an attempt to get a better value for this constant. The error bars are standard errors of the means. For each value of n, I solved 10⁵ TSP instances exactly. All TSP data was computed using Concorde.

references