|
|
This page was last modified 2024-01-21
| |||||||||||||||||||||||||||||||||||||||||||
cliques in G(n,p)G(n,p) is the random graph model in which there are n nodes and each possible edge appears independently with probability p. The clique number of a graph is the size of a largest complete subgraph. Computing the clique number is NP-complete. In Modern graph theory, page 230, Bollobás shows that the clique number of G(n,p) as n→∞ is almost surely d or d+1, where d is the greatest natural number such that binomial(n,d)*p^binomial(d,2)≥log(n). We have 1≤d<n and d=2*log(n)/log(1/p)+O(loglog(n)). How accurate is this formula when n is small? I did some simulations to check this.
|
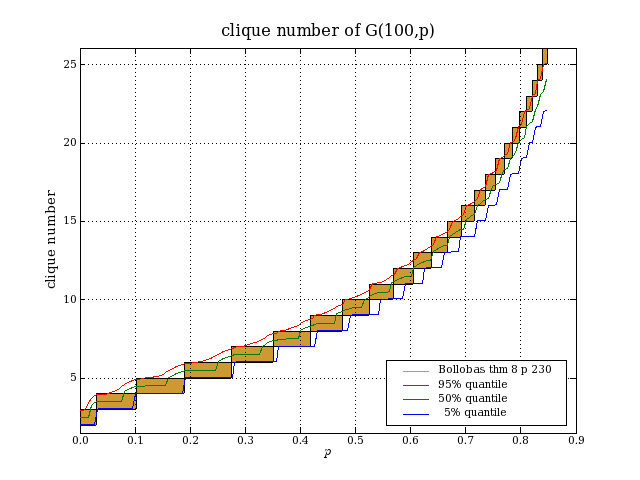
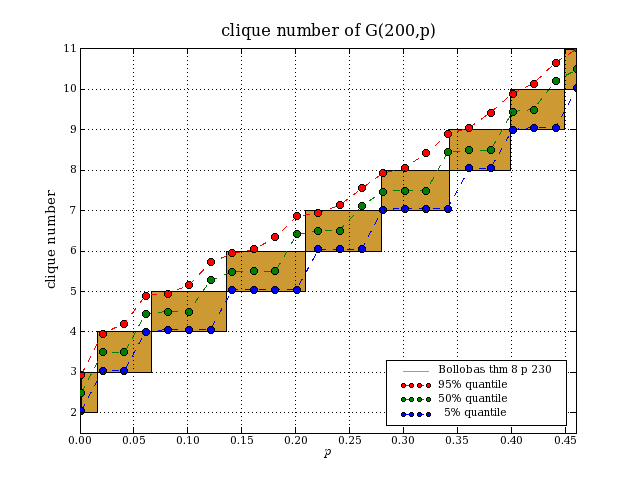
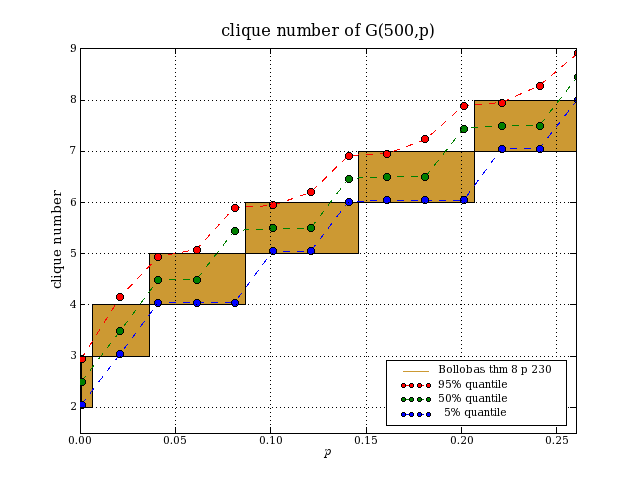 This website uses no cookies. This page was last modified 2024-01-21 10:57
by
This website uses no cookies. This page was last modified 2024-01-21 10:57
by