MSc project ideas - to be supervised by Keith Briggs 2011

I work at BT Research in Martlesham Heath in Suffolk. The ideal arrangement is for you, the MSc student, to work here for all or most of your project. We are at a very lively technology park, and you would have at least daily meetings with me, plenty of desk space and very good computing facilities (i.e. linux). But if this is not feasible, we can negotiate another arrangement.

I like mathematical computing. Most of these projects have that theme. The emphasis is on the concrete. This way of working often involves experimental mathematics, in which we treat the computer as a laboratory for developing and testing conjectures. This does not mean the work lacks rigour - most heuristics on which we work would involve only discrete mathematics, and thus the results are exact. These projects do not generally involve conventional numerical analysis (floating-point errors, and all that). Most of the programming would be in python, C++, and C.

For past projects I have supervised, see here. In principle, projects proposed in past years and not yet done are still available, subject to negotiation. See 2008, 2009, and 2010.

These are only rough sketches for projects. I find that it is better to start this way, and then fine-tune the detail to suit the student's abilities and interests. I prefer to leave some open-endedness, to provide a research challenge. A good MSc project can result in a publication.

1. Distributed heuristics for graph coloring and wireless channel assignment (project taken by Sharon Bullimore)

The world of mobile devices is moving towards autonomous behaviour. This means that no central authority decides things like wireless channel allocation and transmission power level. Devices must behave according to rules which ensure peaceful co-operation. To design these rules is a hard challenge. We work by investigating experimentally (by computer simulation) the basic problem of choosing channels so that the whole system operates without interference. The overall theme is asynchronous distributed heuristics.

In 2010, James Evans did a good project in this area. Since his work, I have become aware of two possible directions for another project.

1. I have proved a new theorem which says that any graph has a χ-coloring in which each node's color is at most its degree plus 1. This should allow us to reduce the size of the search space, and thus speed up the performance of the distributed heuristics, as well as making them more local. This needs to be researched.
2. This paper looks very interesting. Can we compare this method with some of our own?

2. Distributed decision-making (part of QoSMOS)

This project will produce heuristics for decision-making amongst a set of nodes in an uncertain environment. The intended application is to distributed systems of wireless devices which need to choose an operating frequency in a co-operative fashion, even while only possessing incomplete and possibly out-of-date information. It is planned to do the project in two stages:

1. The general picture: we construct a model of interacting nodes (or agents) which share information, along with some indication of the reliability of the information (a recommendation network). The nodes need to come to decisions about allocating shared resources to themselves, by rules (which we must devise) which ensure peaceful coexistence. We will build a software simulation of such a system.
2. We will then apply this general model to the specific problem of wireless channel allocation (possibly also power control etc.) in QoSMOS-type devices. These must use global information (primary user database) and local information (self-sensing, and shared sensing), and synthesize this information before coming to a decision. This decision must be shared with neighbouring nodes. We will test our heuristics on our software platform.

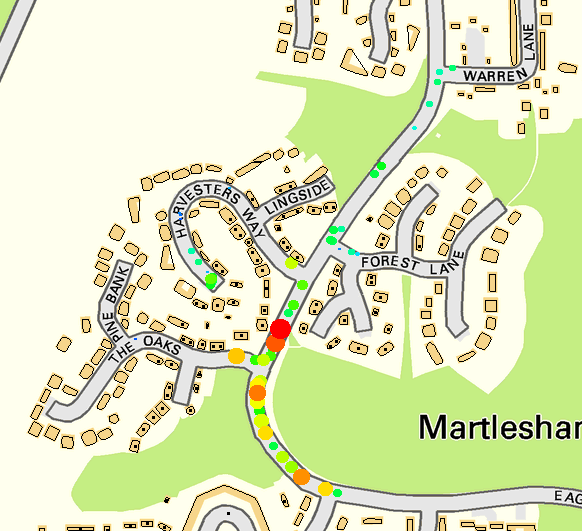
3. Wireless propagation around houses

Wifi is increasing being used outdoors, with products such as BT FON. The signals are at about 2.5GHz, and not too much is known about how walls, trees, etc. affect them. This project will use measurements (which we already have) and try to develop mathematical models. Part of the problem is not being sure exactly where the signal source is. The picture shows points at which one particular homehub was detected, with larger and more red circles for stronger signals. We need a way of assigning this homehub to the most likely house, and then computing estimates for signal loss as a function of distance. This has to be done for cases when there is a house in the way, and when there is not. There is some computational geometry in this project as well as statistical modelling.

4. UHF propagation over hills (taken by Richard Perkins)

There is currently interest in using frequencies in the range 400 to 800 MHz for providing broadband access in rural areas. This is known to work well in flat areas, but over hills there is diffraction which spreads the signal, possibly making it too weak, and we would like to understand this better. We need to work on how the roughness and shape of the hills affects the diffraction, and also how horizontal and vertical polarization differ. The project would use some diffraction theory to develop models appropriate to real situations, and these models will be tested against our own measurement data.

5. Combinatorial optimization for geometric problems

Here's a simple example of the type of problem this project will be concerned with. We want to label points on a maps, subject to the conditions that no pair of labels overlaps, and no label covers a point. The objective is to minimize the total distance of labels from their associated points. This problem is already quite hard, but can be solved exactly (at least for small cases) by branch-and-bound methods. These methods are well worth learning about for their own sake. This project will start by producing a good program for this problem, making it as fast as possible, and then move on to other optimization problems with a geometric flavour. It would be nice to develop a uniform description of problem types and solution methods.

6. Radio signal sensing