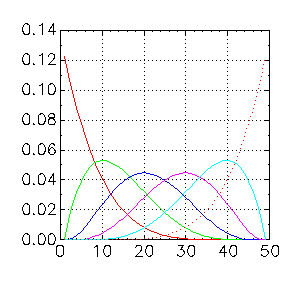
The lottery - an order statistics paradox?

Suppose 6 balls are drawn uniformly from 49 balls (numbered 1 to 49), without replacement.

Sort the balls by the value of their numeric label and let x_i be the value of the ith ranked ball for i from 1 to 6.

Then, for k = 1,2,3,...,49:

(Proof: homework exercise.)
These distributions look like this for i = 1,2,3,4,5,6; and have the mean and mode as in the table. (Proof: another homework exercise.)

i mean mode 1 50/7 1 2 100/7 10 3 150/7 20 4 200/7 30 5 250/7 40 6 300/7 49

In other words, the most likely value for the smallest numbered ball is 1, the most likely value for the second smallest numbered ball is 10, and so on. Everything I have claimed so far is correct.

Therefore, you should put your money on balls 1,10,20,30,40, and 49.