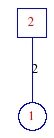
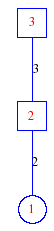
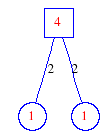
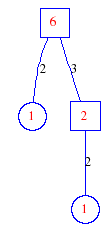
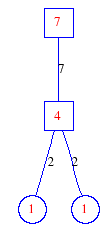
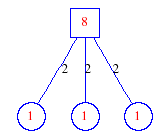
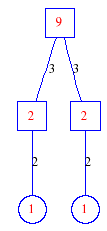
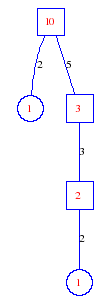
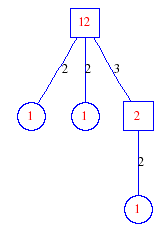
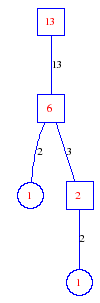
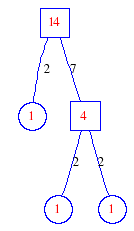
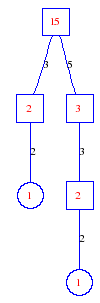
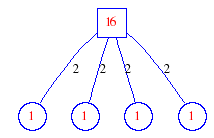
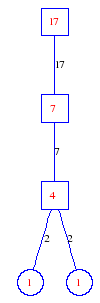
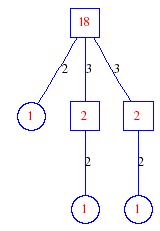
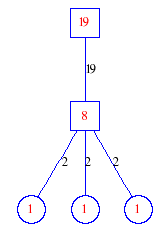
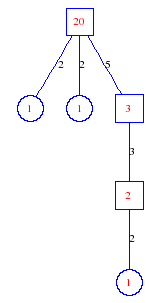
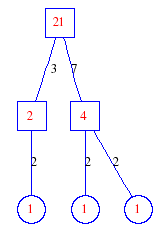
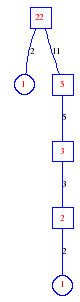
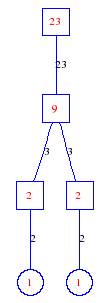
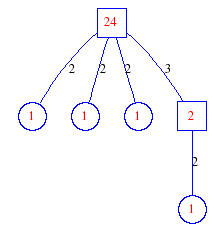
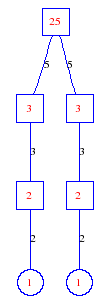
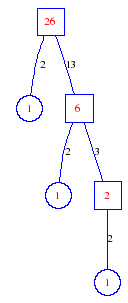
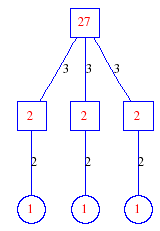
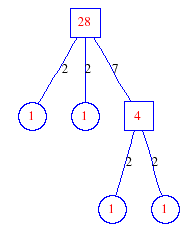
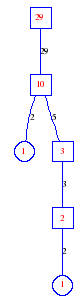
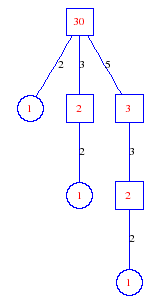
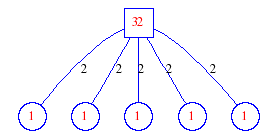
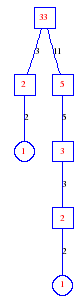
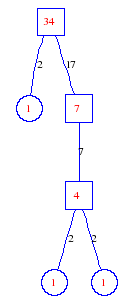
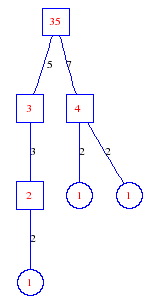
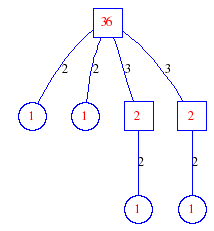
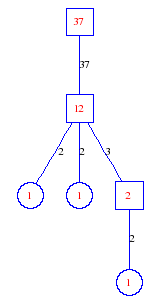
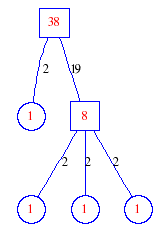
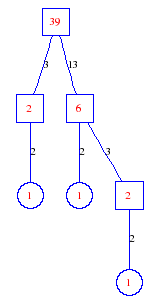
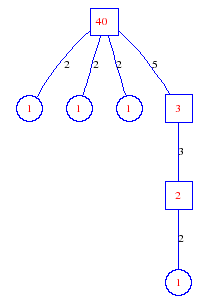
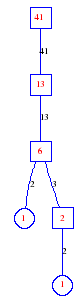
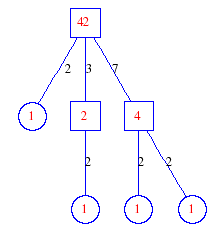
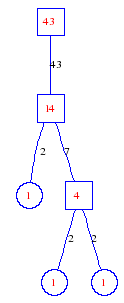
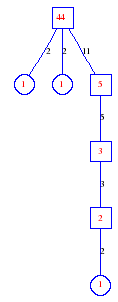
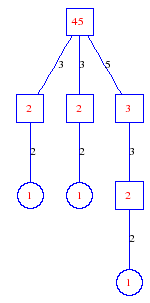
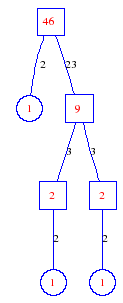
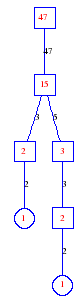
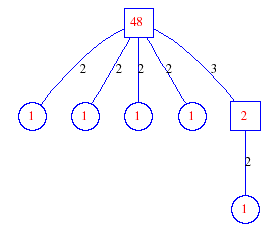
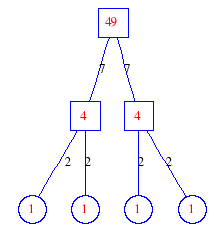
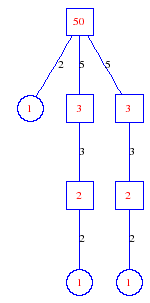
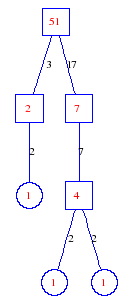
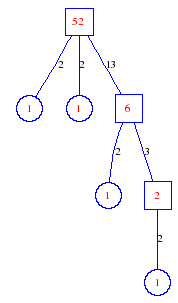
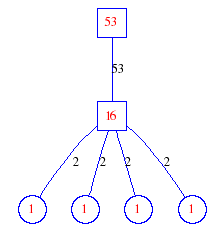
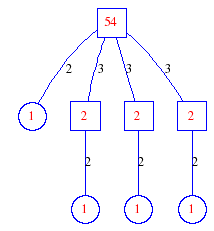
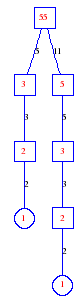
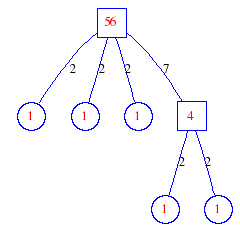
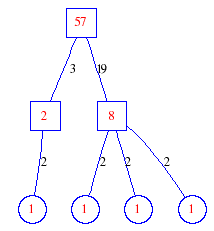
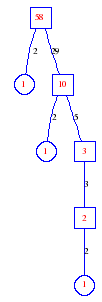
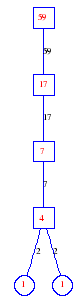
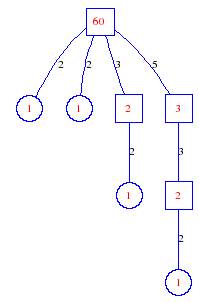
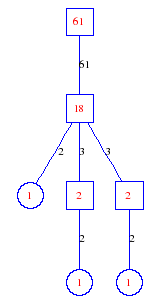
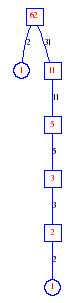
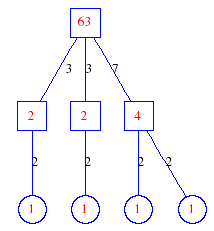
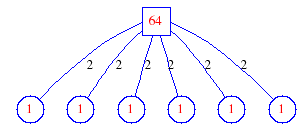
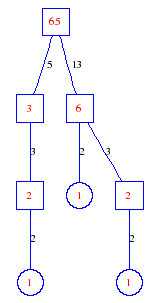
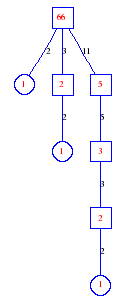
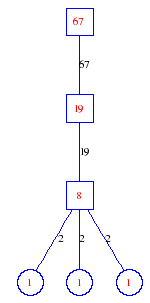
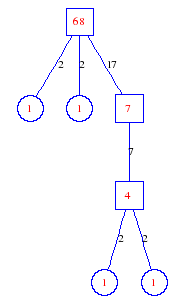
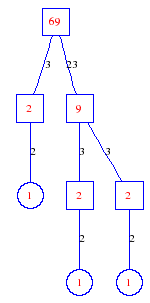
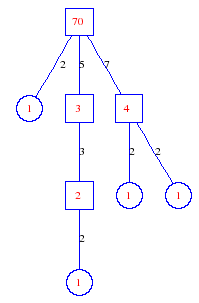
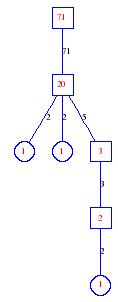
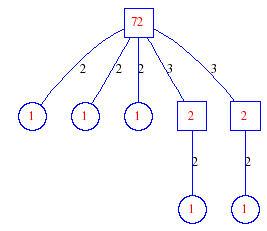
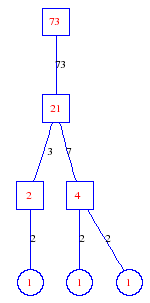
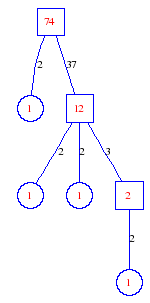
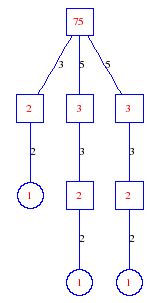
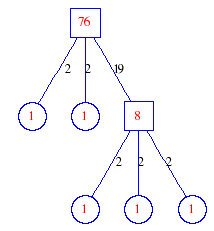
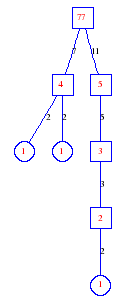
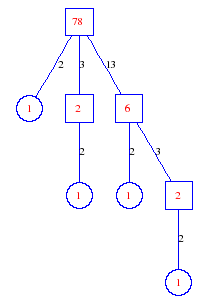
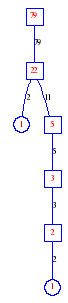
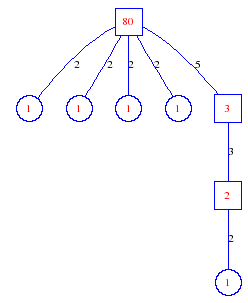
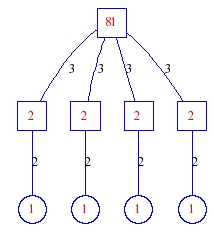
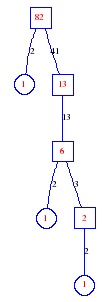
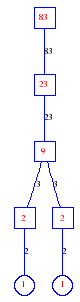
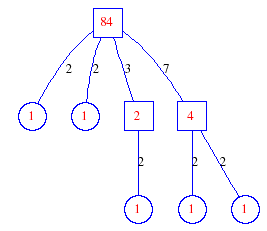
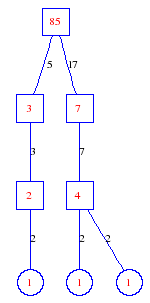
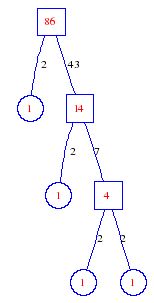
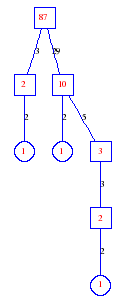
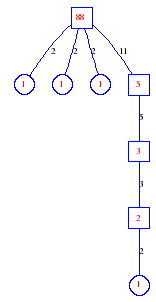
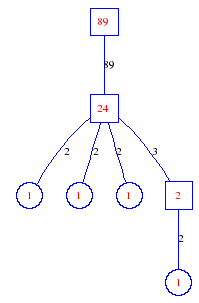
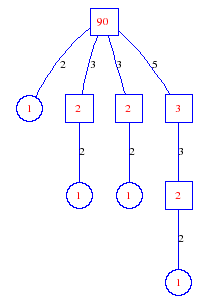
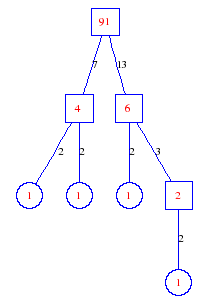
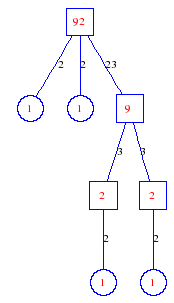
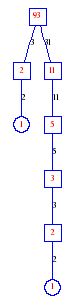
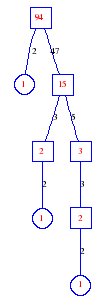
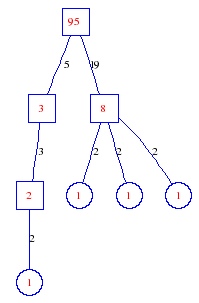
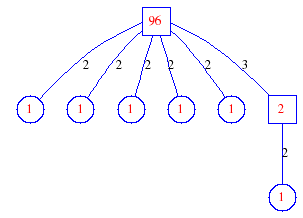
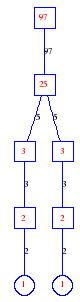
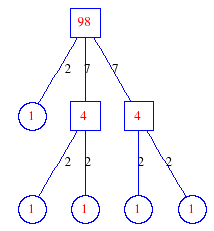
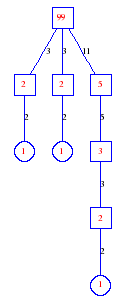
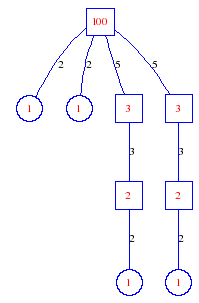
Matula numbers and rooted trees

In SIAM Review volume 10, page 273, D. W. Matula described an interesting bijection between the set of positive integers and the set of rooted trees. This is defined by the following algorithm. Here π(x) is the number of primes less than or equal to x.

matula(n):
  create a node(labelled n)
  for each prime factor p of n:
    add the subtree matula(π(p)), by an edge labelled p
  return the node

exercises

1. give an algorithm for the inverse operation
2. which values of n give line graphs?
3. which values of n give binary trees? [hint]

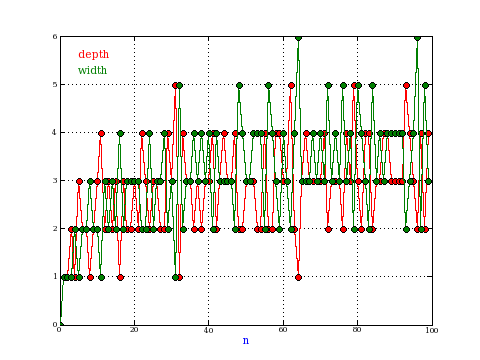
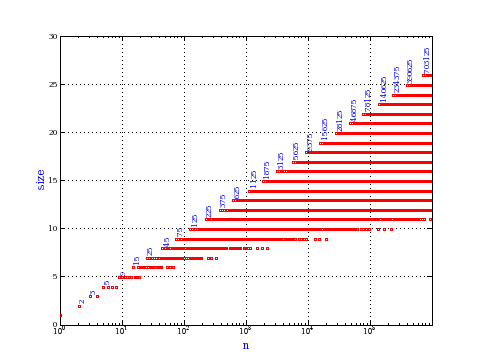
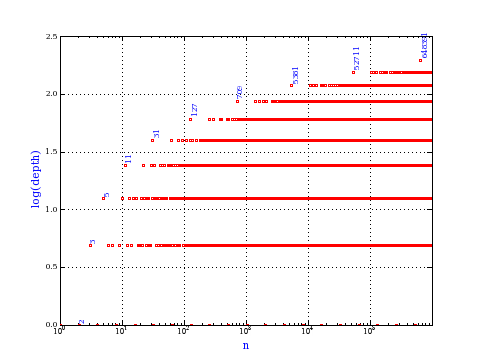
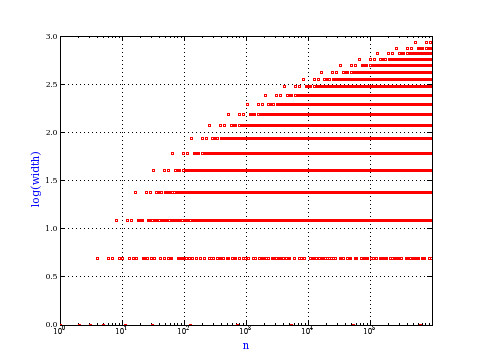
size, depth and width

The size is the number of nodes. The depth of a rooted tree is the maximum distance from the root to a leaf. The width of a rooted tree is the number of leaves.

The plot shows the depth and width of the tree matula(n).

Exercise: how fast do these functions grow? Here is some more data for inspiration. For size and depth, the values of n corresponding to the first increase to a new maximum are labelled.

diagrams of the trees

Here are the Matula trees for n from 1 to 100. The edges are labelled by the prime factors. Leaves are denoted by circles.