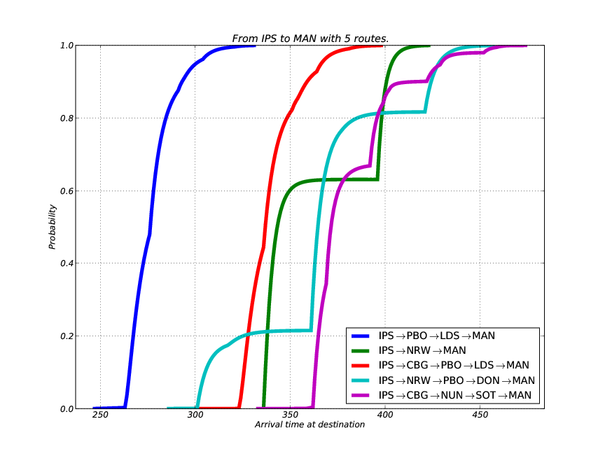
MSc project ideas - to be supervised by Keith Briggs 2010

I work at BT Research in Martlesham Heath. The ideal arrangement is for you, the MSc student, to work here for all or most of your project. We are at a very lively technology park, and you would have at least daily meetings with me, plenty of desk space and very good computing facilities (i.e. linux). But if this is not feasible, we can negotiate another arrangement.

These are only rough sketches for projects. I find that it is better to start this way, and then fine-tune the detail to suit the student's abilities and interests. I prefer to leave some open-endedness, to provide a research challenge. A good MSc project can result in a publication.

I like mathematical computing. Most of these projects have that theme. The emphasis is on the concrete. This way of working often involves experimental mathematics, in which we treat the computer as a laboratory for developing and testing conjectures. This does not mean the work lacks rigour - most algorithms on which we work would involve only discrete mathematics, and thus the results are exact. These projects do not generally involve conventional numerical analysis (floating-point errors, and all that). Most of the programming would be in python and C.

I can probably only supervise 2 (maybe 3) of this projects at one time. So if you are interested, contact me asap!

For past projects I have supervised, see here.

1. Distributed algorithms for graph coloring and wireless channel assignment

The world of mobile devices is moving towards autonomous behaviour. This means that no central authority decides things like wireless channel allocation and transmission power level. Devices must behave according to rules which ensure peaceful co-operation. To design these rules is a hard challenge. We will start by investigating experimentally (by computer simulation) two basic problems: to choose channels so that the whole system operates without interference; and, if this is not possible, to choose channels so that total interference is minimized. The overall theme is asynchronous distributed algorithms.

2. Statistics of train arrival delays

A previous project looked at statistical models in the delay to departure time of trains. An interesting result was obtained - that the delays follow a q-exponential distribution. This project would do the same thing for arrival delays, and, by extension, we can then study the distribution of trip delays. These statistical models have important applications to algorithms for optimal trip planning in the presence of random delays. I already have developed software for this problem, and part of the project would be to add the new arrival time model to the software. The figure shows a typical output of the current program (written by my student Kin Po Tam).

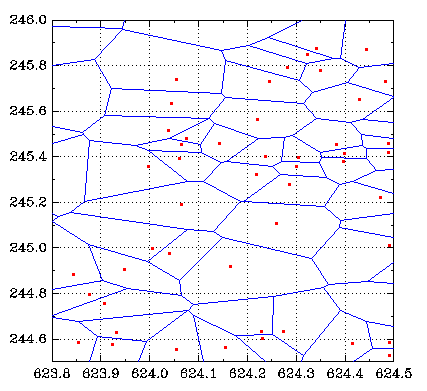
NB: if you are interested in this project, please tell me asap, because we should start collecting data well before the project starts.

3. Computational geometry for wireless homehub applications

Wireless systems are evolving towards a smaller cell-size, so that we now think of house-sized cells. To model and simulate such systems requires models of house-density distributions. This information is not readily available, but a good proxy is the postcode database. This project would look at the Voronoi geometry of the postcode distribution (the figure shows an example from the Ipswich area), and calculate statistics relevant to wireless systems, such as distribution of housing density, and fractional coverage as a function of transmit power.

4. Sensing techniques for estimating the number of transmitters

The world of mobile devices is moving towards autonomous behaviour. It would be useful in practice if a device knew the number of other transmitters in its neighbourhood, so that it can avoid interfering with them (this is part of what is called cognitive radio). This estimation can be attempted by a small group of devices co-operating, so that they all measure received signal strengths and share their readings. This amount to estimating the power profile as a function of position, and from this optimization methods can be used to find the number of transmitters.

This project is very speculative and it is quite uncertain whether any method will work well in practice. Anyone selecting this project will need lots of imagination and willingness to try many alternative algorithms!

5. Satisfiability algorithms (SAT)

The SAT (satisfiability) problem is a very basic problem in logic: to determine whether a given Boolean function has an input which makes the output true. There are many good heuristics now available to solve SAT problems, and many practical problems are equivalent to, and can be translated into SAT.

This project would make a comparison of available solvers, and study their application to some practical problems in optimization, scheduling, and graph coloring. The fun part would be writing programs to translate these into SAT!

6. Maximum-likelihood period estimation

This project would be to study the paper (only 4 pages!):

Maximum-likelihood period estimation from sparse, noisy timing data, by Robby McKilliam and I. Vaughan L. Clarkson

and write a program to implement the method. This is an important problem area with applications in telecoms.

7. Haartsen's Novel wireless modulation technique based on noise

In this paper, Haartsen has proposed a wireless modulation technique based on noise. This project would build software simulators for this system, and investigate its performance, which would be compared with the theory.

8. Fast counting

This project is inspired by the paper HyperLoglog: the analysis of a near-optimal cardinality estimation algorithm of Flajolet et al. How do we estimate (rapidly, and with minimal storage) the number of distinct items in a very large set (or data stream)? In other words, the problem concerns estimating the cardinality of a multiset. Flajolet et al. previously developed their loglog algorithm, and I worked on an efficient C implementation of this. They have now improved this with the hyperloglog algorithm, and this project would be to implement this and compare its performance in practice with alternatives.

The algorithm should have practical applications in informatics; for example, counting the number of different packet types in a network.

9. Fast random selection

Consider the problem: a large number N of objects are presented to us one by one, and we wish to either:

The problem becomes hard to solve efficiently when p is small, because to generate a random number which usually results in a rejection is inefficient. It would be better to skip over a block of items. Ways to do these were proposed by Vitter in ACM Trans Math Soft 13, 58 (1987).

This project would investigate these methods and check their efficiency in practice. There are applications to the generation of large random graphs.