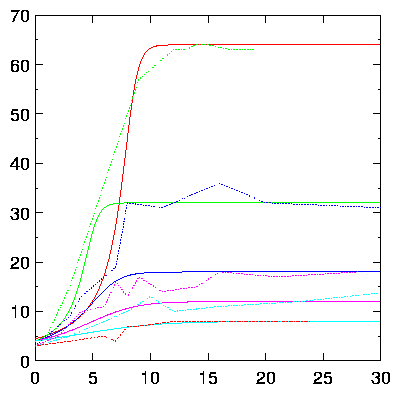
|
|
This page was last modified 2024-01-21
| |||||||||||||||||||||||||||||||||||||||||||
W-ology, or, some exactly solvable growth models
by Keith Briggs (formerly at Department of Plant Sciences,
University of Cambridge,
Downing St.,
Cambridge CB2 3EA. Revised 1999 Nov 12; font adjustments 2005 July 11) `To give full growth to that which still doth grow?' - Shakespeare, Sonnet CXV
IntroductionAim of these notes: to show how some generalizations of logistic growth laws have elegant analytic solutions and speculate on their applications to modelling. Lambert's W function is defined by
Useful formulas
Differential equationsIt is usually considered that the most general exactly solvable growth model is that of Richards:
(ν not 0, ν> -2) for which the solution is
with J a function of Κ,ν and y(0). Instead, I wish to consider models of the form
etc. These allow us to give explicitly the solution of the initial value problem
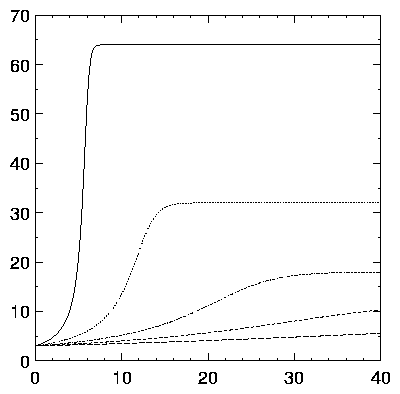
A very rough fit of equation (4) to some onion plant growth data is shown in Figure 2. No attempt has been made to optimize the parameters.
Another differential equation, which can be interpreted as having a time-dependent growth rate, is
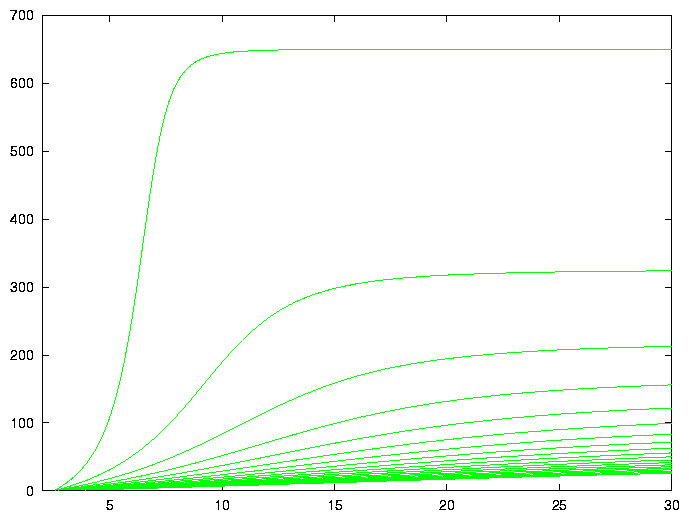
Lotka-Volterra modelsThe two-species model
Take-home messageDon't assume that only solutions expressible with standard elementary transcendental functions are the only useful ones!
A numerical algorithm for W
/* ANSI C code for W(x). K M Briggs 98 Feb 12
http://www-epidem.plantsci.cam.ac.uk/~kbriggs/LambertW.c
Based on Halley iteration. Converges rapidly for all valid x. */
double W(const double x) {
int i; double p,e,t,w,eps=4.0e-16; /* eps=desired precision */
if (x<-0.36787944117144232159552377016146086) {
fprintf(stderr,"x=%g is < -1/e, exiting.\n",x); exit(1); }
if (0.0==x) return 0.0;
/* get initial approximation for iteration... */
if (x<1.0) { /* series near 0 */
p=sqrt(2.0*(2.7182818284590452353602874713526625*x+1.0));
w=-1.0+p-p*p/3.0+11.0/72.0*p*p*p;
} else w=log(x); /* asymptotic */
if (x>3.0) w-=log(w);
for (i=0; i<20; i++) { /* Halley loop */
e=exp(w); t=w*e-x;
t/=e*(w+1.0)-0.5*(w+2.0)*t/(w+1.0); w-=t;
if (fabs(t)<eps*(1.0+fabs(w))) return w; /* rel-abs error */
} /* never gets here */
fprintf(stderr,"No convergence at x=%g\n",x); exit(1);
}
Bibliography
I've tried to make these notes self-contained, so all you should need is...
[1] Briggs, K. M. W-ology, or, some exactly solvable growth models
Footnotes:1: Johann Heinrich Lambert: born 1728 Aug 26 in Mülhausen, Alsace;
died 1777 Sep 25 in Berlin, Prussia.
Lambert was a colleague of Euler and Lagrange at the Berlin Academy of Sciences.
Amongst other achievements, he was the first to provide a rigorous proof that π is irrational.
This website uses no cookies. This page was last modified 2024-01-21 10:57
by | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||