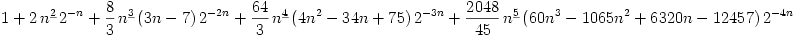Combinatorial graph theory
Introduction
This page collects together some data from my own computations, enumerating
various types of graphs.
number of graphs on n nodes with edge chromatic number k
k | n= 1 2 3 4 5 6 7 8 9 10
--------------------------------------------------------
0 | 1 1 1 1 1 1 1 1 1 1
1 | 0 1 1 2 2 3 3 4 4 5
2 | 0 0 1 3 5 10 15 26 37 58
3 | 0 0 1 5 14 46 123 375 1061 3331
4 | 0 0 0 0 10 58 347 2130 14039 103927
5 | 0 0 0 0 2 38 392 4895 68696 1140623
6 | 0 0 0 0 0 0 159 3855 113774 3953535
7 | 0 0 0 0 0 0 4 1060 64669 4607132
8 | 0 0 0 0 0 0 0 0 12378 1921822
9 | 0 0 0 0 0 0 0 0 9 274734
10 | 0 0 0 0 0 0 0 0 0 0
number of connected graphs on n nodes with edge chromatic number k
k | n= 1 2 3 4 5 6 7 8 9 10
--------------------------------------------------------
0 | 1 0 0 0 0 0 0 0 0 0
1 | 0 1 0 0 0 0 0 0 0 0
2 | 0 0 1 2 1 2 1 2 1 2
3 | 0 0 1 4 8 26 58 185 500 1677
4 | 0 0 0 0 10 48 279 1715 11464 87114
5 | 0 0 0 0 2 36 352 4463 63363 1066463
6 | 0 0 0 0 0 0 159 3696 109760 3835747
7 | 0 0 0 0 0 0 4 1056 63605 4541399
8 | 0 0 0 0 0 0 0 0 12378 1909444
9 | 0 0 0 0 0 0 0 0 9 274725
10 | 0 0 0 0 0 0 0 0 0 0
number of graphs with specified clique and chromatic number
The following data was computed with my own codes for clique and chromatic number, together with nauty. Some of them extend sequences in the OEIS, in which case the A-number is given; others were new sequences before several were added to OEIS in February 2007.
number of graphs on n nodes with chromatic number k
n = 1 2 3 4 5 6 7 8 9 10
k ----------------------------------------------------------
2 0 1 2 6 12 34 87 302 1118 5478 A076278
3 0 0 1 3 16 84 579 5721 87381 2104349 A076279
4 0 0 0 1 4 31 318 5366 155291 7855628 A076280
5 0 0 0 0 1 5 52 867 28722 1919895 A076281
6 0 0 0 0 0 1 6 81 2028 115391 A076282
7 0 0 0 0 0 0 1 7 118 4251
8 0 0 0 0 0 0 0 1 8 165
9 0 0 0 0 0 0 0 0 1 9
10 0 0 0 0 0 0 0 0 0 1
11 0 0 0 0 0 0 0 0 0 0
number of graphs on n nodes with clique number k
n = 1 2 3 4 5 6 7 8 9 10
k ----------------------------------------------------------
2 0 1 2 6 13 37 106 409 1896 12171 A052450
3 0 0 1 3 15 82 578 6021 101267 2882460 A052451
4 0 0 0 1 4 30 301 4985 142276 7269487 A052452
5 0 0 0 0 1 5 51 842 27107 1724440 A077392
6 0 0 0 0 0 1 6 80 1995 112225 A077393
7 0 0 0 0 0 0 1 7 117 4210 A077394
8 0 0 0 0 0 0 0 1 8 164
9 0 0 0 0 0 0 0 0 1 9
10 0 0 0 0 0 0 0 0 0 1
number of connected graphs on n nodes with chromatic number k
The first row is the same as the number of connected bipartite graphs on n nodes.
n= 1 2 3 4 5 6 7 8 9 10
k ------------------------------------------------------------
2| 0 1 1 3 5 17 44 182 730 4032 A005142
3| 0 0 1 2 12 64 475 5036 80947 2010328
4| 0 0 0 1 3 26 282 5009 149551 7694428
5| 0 0 0 0 1 4 46 809 27794 1890221
6| 0 0 0 0 0 1 5 74 1940 113272
7| 0 0 0 0 0 0 1 6 110 4125
8| 0 0 0 0 0 0 0 1 7 156
9| 0 0 0 0 0 0 0 0 1 8
10| 0 0 0 0 0 0 0 0 0 1
number of connected triangle-free graphs on n nodes with chromatic number k
The first row is the same as the number of connected bipartite graphs on n nodes.
n= 1 2 3 4 5 6 7 8 9 10 11 12 13 14
k -----------------------------------------------------------------------------------------
2| 0 1 1 3 5 17 44 182 730 4032 25598 212780 2241730 31193324 A005142
3| 0 0 0 0 1 2 15 85 650 5800 65243 931258 17182237 414512599
4| 0 0 0 0 0 0 0 0 0 0 1 23 1085 75127
number of connected graphs on n nodes with clique number k
The first row is the same as the number of connected triangle-free graphs on n unlabeled nodes.
n= 1 2 3 4 5 6 7 8 9 10
k ------------------------------------------------------------
2| 0 1 1 3 6 19 59 267 1380 9832 A024607
3| 0 0 1 2 11 63 477 5339 94535 2774240
4| 0 0 0 1 3 25 266 4646 136935 7121703
5| 0 0 0 0 1 4 45 785 26205 1696407
6| 0 0 0 0 0 1 5 73 1908 110140
7| 0 0 0 0 0 0 1 6 109 4085
8| 0 0 0 0 0 0 0 1 7 155
9| 0 0 0 0 0 0 0 0 1 8
10| 0 0 0 0 0 0 0 0 0 1
number of biconnected graphs on n nodes with chromatic number k
n= 1 2 3 4 5 6 7 8 9 10
k ---------------------------------------------------------
2| 0 0 0 1 1 5 8 42 146 956
3| 0 0 1 1 6 30 232 2762 50814 1420183
4| 0 0 0 1 2 17 189 3627 118114 6530233
5| 0 0 0 0 1 3 34 627 23262 1686975
6| 0 0 0 0 0 1 4 59 1631 101409
7| 0 0 0 0 0 0 1 5 92 3643
8| 0 0 0 0 0 0 0 1 6 135
9| 0 0 0 0 0 0 0 0 1 7
10| 0 0 0 0 0 0 0 0 0 1
number of biconnected triangle-free graphs on n nodes with chromatic number k
n= 1 2 3 4 5 6 7 8 9 10 11 12 13 14
k --------------------------------------------------------------------------------
2| 0 0 0 1 1 5 8 42 146 956 6643 65921 818448 13442572
3| 0 0 0 0 1 1 8 36 269 2418 29216 458445 9373692 249530113
number of connected 4-cycle-free graphs on n nodes with clique number k
n= 1 2 3 4 5 6 7 8 9 10 11 12 13 14
k ---------------------------------------------------------------------------------------
2| 0 1 1 2 4 8 18 47 137 464 1793 8167 43645 275480
3| 0 0 1 1 4 11 39 139 603 2925 16709 112054 888615 8321364
tables of numbers of unlabelled (US: unlabeled) graphs
This sequence is A000088 in OEIS.
The previously best available data was to 68 nodes: Klas Markström's data.
I have now reached 140 nodes by a sum-over-partitions method. For details of
the method see W. Oberschelp, Math. Annalen, 174, 53-78.
The following file counts graphs by number of nodes only: oberschelp-gmp-02.500.
The columns are:
1: n: number of nodes
2: np: number of partitions p(n) of n
3: ng: number g(n) of unlabelled graphs on n nodes
5: nc: number c(n) of connected unlabelled graphs on n nodes
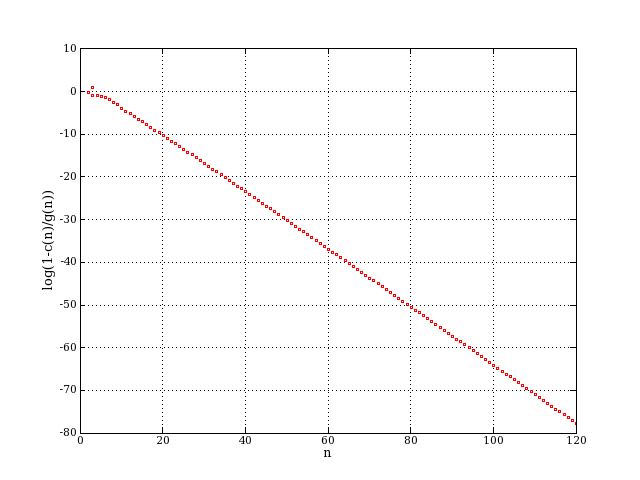
7: log(1-fc): log(1-c(n)/g(n)). The fraction connected tends to 1
8: sqrtlogng: sqrt(log(g(n))). This is a function of the growth rate
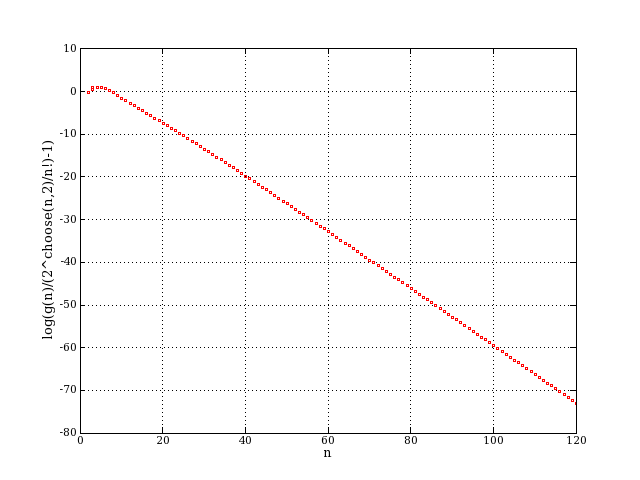
9: log(ng/asymp-1): log(g(n)/(2^choose(n,2)/n!)-1). This compares with the
asymptotic number
Here are plots of log(1-c(n)/g(n)) and log(g(n)/(2^choose(n,2)/n!)-1), to
show the rate of approach to minus infinity of these quantities.
asymptotics of numbers of unlabelled graphs
I have improved the formula of Harary & Palmer (eq. 9.1.25, page 199)
to include all terms up to k=11. The displayed equation gives the asymptotic expansion of g(n)/f(n), where f(n) is 2^{n(n-1)/2}/n!. The underline indicates
a falling factorial.
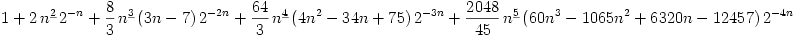
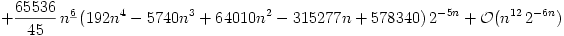
counts of numbers of unlabelled graphs by edges
The following files count graphs by number of nodes and number of edges.
The columns are:
1: number of nodes
2: number of edges
3: number of connected unlabelled graphs
4: total number of unlabelled graphs
5: fraction of connected graphs (column3/column4)
These were computed using this
maple program
by Brendan McKay, from the website of Gordon Royle.
diagrams of graphs
These are pdfs: with acrobat reader, zoom in with ctrl+.
The topologies were computed using the
nauty program by Brendan McKay
and the layouts created with
graphviz.
I wrote python programs to interface these and produce the pdfs.
plots of graph counts
tables of numbers of labelled graphs
I have data available for up to 2000 nodes, and excess up to 8.
labelled planar graphs
I have computed the number of labelled planar graphs up to 42 nodes,
using a recurrence of Clemens Groepl:
data
useful external links
This website uses no cookies. This page was last modified 2024-01-21 10:57
by  .
.