The very_nauty graph library - version 1.1

• cliques in G(n,p)
• data on chromatic number and clique number
• graph theory and Lambert's W function
• number of graphs on n nodes with chromatic number k
• number of graphs on n nodes with clique number k

basic graph functions and macros

All graphs are simple and undirected. They are represented internally by dynamically allocated adjacency lists.

graph_t	type of a graph
void set_adj_list_initial_size(size_t sz)	set initial size of adjacency lists (defaults to 8)
graph_t graph_new(unsigned int n);	return a new empty graph with n nodes labelled 0..n-1
void graph_clear(graph_t g);	destroy a graph
void graph_empty(graph_t g);	set to the empty graph
void graph_add_edge(graph_t g,node_t i,node_t j);	add undirected edge i-j to the graph
void graph_del_edge(graph_t g,node_t i,node_t j);	delete edge i-j from the graph
int graph_has_edge(graph_t g,node_t i,node_t j);	1 if edge i-j is present in g, else 0
void graph_add_node(graph_t g);	add a node to the graph
nnodes(g)	number of nodes in g
nedges(g)	number of edges in g
graph_node_degree(graph_t g, node_t i);	degree of a node
int graph_min_degree(graph_t g);	minimum degree of a node in g
int graph_max_degree(graph_t g);	maximum degree of a node in g
double graph_mean_degree(graph_t g);	return mean degree of the nodes of g
void graph_show(graph_t g);	list edges of g to stdout
void graph_make_dotfile(graph_t g, char* fn);	write a dotfile suitable for processing by graphviz
void graph_make_dotfile_colored(graph_t g, char* fn);	write a colored dotfile suitable for processing by graphviz
void graph_to_dimacs(graph_t g, char* fn);	write graph to a file named fn in DIMACS format
void graph_to_theta(graph_t g, char* fn);	write graph to a file named fn in a format suitable for reading by Benson's Lovász theta program
int graph_nclusters(graph_t g);	the number of clusters (connected components) in g
int graph_connected(graph_t g);	1 if g is connected, else 0
cluster(g,i)	cluster to which node i belongs (valid only after a call to graph_greedy_color or graph_nclusters)
int* graph_cluster_sizes(graph_t g)	return a (0-terminated) list of cluster sizes, largest first
int graph_max_cluster(graph_t g)	size of largest cluster (graph is connected if this equals nnodes(g))

random graph generation

For more than a few graphs, it's better to use the iterators in the next section (especially for GRG).

void graph_gnp(graph_t g, double p);	generate an instance of the random graph G{n,p}
void graph_gnm(graph_t g, int m);	generate an instance of the random graph G(n,m)
void graph_grg(graph_t g, double r);	generate an instance of the geometric random graph GRG(n,r). This has n nodes in the unit square, with each pair linked if their separation is less than r
void graph_lognormal_grg(graph_t g, double r, double alpha);	nodes a distance d apart are joined with probability (1-erf(log(d/r)/alpha))/2
void graph_grg_torus(graph_t g, double r);	as graph_grg, but in a unit-area torus instead of a square
void graph_lognormal_grg_torus(graph_t g, double r, double alpha);	nodes a torus distance d apart are joined with probability (1-erf(log(d/r)/alpha))/2

random graph iterators

When using these, an indefinitely large sample is generated from the specified ensemble, and f is called for each graph. f should return 0 to terminate the iteration. Arbitrary client data or parameters may be passed to f through cd.

graph_gnp_iterator(unsigned int n, double p, int f(graph_t,int,void*), void* cd);	G{n,p}
graph_gnm_iterator(unsigned int n, unsigned long m, int f(graph_t,int,void*), void* cd);	G(n,m)
int graph_grg_torus_iterator(unsigned int n, double r, int f(graph_t,int,void*), void* cd);	GRG(n,r)
int graph_random_line_graph_iterator(unsigned int nlines, int f(graph_t,int,void*), void* cd)	model: place nlines dots uniformly in the unit square; put a line of random slope through each dot; intersections of these lines are the nodes of the graph; line segments between intersections are the edges of the graph
int graph_random_line_poisson_graph_iterator(double tau, int f(graph_t,int,void*), void* cd)	as above, but a Poisson number (mean=4*tau/pi) of nodes in the square

clique number (ω) computation

int graph_clique_number(graph_t g);

compute the exact clique number of g. Warning: this can take a long time for large graphs

complementation and switching

void graph_complement(graph_t gc, graph_t g);	complement g
void graph_local_complement(graph_t g, node_t i);	in-place local complementation at node i; i.e. subgraph N_i(g) is complemented, where N_i(g) is the set of neighbours of i
void graph_switching(graph_t g, node_t i);	in-place switching at node i; i.e. flip dyads incident on i

coloring and chromatic number (χ) computation

int graph_greedy_color(graph_t g,int perm[]);	color the nodes of g in the node order given by perm, which must be a permutation of 0..nnodes(g)-1, or NULL, in which case the identity permutation is used. This returns a rapidly computable upper bound to the chromatic number
int graph_sequential_color(graph_t g,int perm[],int ub);	color the nodes of g in node order given by perm, aborting as soon as more than ub colors are used (in which case -1 is returned). This returns an upper bound to the chromatic number
int graph_sequential_color_repeat(graph_t g, int n);	color g's nodes n times in different random orders, and return the number of colors used in the best coloring found. The larger n is, the tighter the upper bound to the chromatic number is likely to be
int graph_chromatic_number(graph_t g,clock_t timeout);	compute the exact vertex chromatic number of g. If the timeout value (in seconds) is not zero and is reached, return -1. Warning: this can take a long time for large graphs
int graph_edge_chromatic_number(graph_t g,clock_t timeout);	compute the exact edge chromatic number of g. If the timeout value (in seconds) is not zero and is reached, return -1. Warning: this can take a long time for large graphs
color(g,i)	color of node i in g (valid only after calling one of the coloring functions)
int graph_ncolors(graph_t g);	number of colors used in a coloring of g
int graph_check_coloring(graph_t g);	check that a node coloring is valid

histogram functions

Some convenience functions for collecting statistics (data restricted to non-negative integer values)...

histogram_t histogram_new(char* lbl);	make a new histogram labelled lbl
void histogram_empty(histogram_t);	reset a histogram to all zeros
void histogram_add(histogram_t h, int i);	add datum i to h
void histogram_clear(histogram_t h);	destroy h
void histogram_show(histogram_t h);	print h to stdout
void histogram_write(FILE*,histogram_t h);	write h to file
double histogram_mean(histogram_t h);	compute the mean of h
int histogram_max(histogram_t h);	maximum value in h
double histogram_variance(histogram_t h);	compute the variance of h
unsigned int histogram_mode(histogram_t h);	compute the mode of h
int histogram_biggest_done(histogram_t h, double eps);	return 1 if the modal value has relative standard error less than eps, else 0
int histogram_mean_done(histogram_t h, double eps);	return 1 if the mean has relative standard error less than eps, else 0
double histogram_quantile(histogram_t h, double q);	compute the qth quantile of h (q=0.5 for the median)
histogram_t graph_geng_reader(FILE* f, int op(graph_t), char* lbl);	iterate over graphs in file f (in graph6 or sparse6 format), applying op to each and returning a histogram
histogram_t graph_showg_reader(FILE* f, int op(graph_t), char* lbl);	iterate over graphs in file f (in "showg -l0 -e" format), applying op to each and returning a histogram

download & installation

• get very_nauty-1.1.tgz
  
• tar zxf very_nauty-1.1.tgz
• cd very_nauty-1.1
• make
• sudo make install

simple library usage example

• cat example_03.c

  #include "vn_graph.h"
  
  int main() {
    graph_t g=graph_new(5);
    graph_add_edge(g,0,1);
    graph_add_edge(g,0,2);
    graph_add_edge(g,0,3);
    graph_add_edge(g,0,4);
    graph_add_edge(g,1,4);
    graph_show(g);
    printf("chi=%d\n",graph_chromatic_number(g,0));
    graph_make_dotfile_colored(g,"example_03.dot");
    printf("number of clusters=%d\n",graph_nclusters(g));
    graph_add_node(g);
    printf("nnodes=%d number of clusters=%d\n",nnodes(g),graph_nclusters(g));
    graph_clear(g);
    return 0;
  }
  

• gcc -I/usr/local/include example_03.c -o example_03 -L/usr/local/lib -lvn_graph -lm
• ./example_03

  0: 1 2 3 4
  1: 0 4
  2: 0
  3: 0
  4: 0 1
  chi=3
  example_03.dot written: now do "neato -Tps example_03.dot | gv -"
  number of clusters=1
  nnodes=6 number of clusters=2
  

• neato -Tpng example_03.dot > example_03.png

  

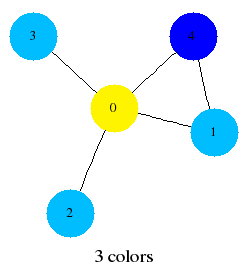
stand-alone programs

The programs vn_graph_omega and vn_graph_chi are provided for computing clique and (vertex) chromatic number of geng output. Also vn_graph_chi_dash computes the edge chromatic number.

Examples:

• Compute the clique number of all 8-node graphs:

  kbriggs:~/very_nauty-1.1> geng 8 | time ./vn_graph_omega
  >A geng -d0D7 n=8 e=0-28
  >Z 12346 graphs generated in 0.03 sec
  graph_omega 12346 items; mode=3 average=3.528997 variance=0.4996 stdev=0.7069 stderr=0.006362
   1          1   0.000081    0.008% se=nan
   2        409   0.033128    3.313% se=0.0104
   3       6021   0.487688   48.769% se=0.000793
   4       4985   0.403775   40.377% se=0.0012
   5        842   0.068200    6.820% se=0.000608
   6         80   0.006480    0.648% se=0.000205
   7          7   0.000567    0.057% se=6.62e-05
   8          1   0.000081    0.008% se=nan
  0.15user 0.02system 0:00.25elapsed 67%CPU
  

• Estimate the distribution of chromatic number in G(50,1/5):

  kbriggs:~/very_nauty-1.1> genrang -P20/100 50 10000 | time ./vn_graph_chi
  graph_chi 10000 items; mode=5 average=5.010700 variance=0.01239 stdev=0.1113 stderr=0.001113
   4          9   0.000900    0.090% se=0.000298
   5       9875   0.987500   98.750% se=1.26e-05
   6        116   0.011600    1.160% se=0.000198
  11.56user 0.33system 0:13.53elapsed 87%CPU
  

• Compute the chromatic number of all 10-node connected graphs regular of degree 4:

  kbriggs:~/very_nauty-1.1> geng -c -d4 -D4 10 | ./vn_graph_chi
  >A geng -cd4D4 n=10 e=20
  >Z 59 graphs generated in 0.01 sec
  graph_chi 59 items; mode=4 average=3.491525 variance=0.2887 stdev=0.5373 stderr=0.06995
   2          1   0.016949    1.695% se=nan
   3         28   0.474576   47.458% se=0.0207
   4         30   0.508475   50.847% se=0.0246
  

• Compute the edge chromatic number of all 10-node connected triangle-free graphs:

  kbriggs@europa:~/very_nauty-1.1> geng -c -t 10 | time ./vn_graph_chi_dash
  >A geng -ctd1D9 n=10 e=9-25
  >Z 9832 graphs generated in 0.04 sec
  graph_chi_dash 9832 items; mode=4 mean=4.440602 var=0.5836 stdev=0.7639 stderr=0.007704
   2          2   0.000203    0.020% se=4.48e-05
   3        694   0.070586    7.059% se=0.000612
   4       4953   0.503763   50.376% se=0.00121
   5       3435   0.349369   34.937% se=0.000571
   6        659   0.067026    6.703% se=0.00225
   7         80   0.008137    0.814% se=0.00719
   8          8   0.000814    0.081% se=0.0323
   9          1   0.000102    0.010% se=nan
  0.14user 0.00system 0:00.26elapsed 55%CPU
  

acknowledgements

• Brendan McKay for nauty, from which I borrowed code to read graph6 and sparse6 format.
• Kevin O'Neill for the original version of the exact clique number algorithm. I modified this to use dynamic memory allocation and made various other improvements.
• Michael Trick for the original version of the exact chromatic number algorithm. I modified this to use dynamic memory allocation and made various other improvements.
• Linlin Song for beta-testing