Keith Briggs: : xrc manpage

Keith Briggs

This page was last modified 2024-01-21

home
·	publications
·	thesis
·	talks
·	meetings
·	records
·	maths notes
·	software «
·	languages
·	music
·	travel
·	cv
·	memberships
·	students
·	maps
·	place-names
·	people
·	photos
·	links
·	ex libris
·	site map

xrc-1.1

NAME

xr - C library of exact real functions

SYNOPSIS

#include <xr.h>

int xr_get_b ();
void xr_set_b (int b);

xr_t xr_init (long a, long b);
xr_t xr_set (const xr_t a);
void xr_free (const xr_t x);

xr_t xr_abs (const xr_t x);
xr_t xr_neg (const xr_t x);
xr_t xr_recip (const xr_t x);
xr_t xr_sqrt (const xr_t x);
xr_t xr_sqr (const xr_t x);

xr_t xr_iadd (const long x, const xr_t y);
xr_t xr_isub (const long x, const xr_t y);
xr_t xr_imul (const long x, const xr_t y);

xr_t xr_subi (const xr_t x, const long y);
xr_t xr_divi (const xr_t x, const long y);
xr_t xr_powi (const xr_t xx, long n);
xr_t xr_root (const xr_t xx, long n);

xr_t xr_add (const xr_t x, const xr_t y);
xr_t xr_sub (const xr_t x, const xr_t y);
xr_t xr_mul (const xr_t x, const xr_t y);
xr_t xr_div (const xr_t x, const xr_t y);

xr_t xr_pi (void);
xr_t xr_exp (const xr_t x);

int xr_cmp (xr_t a, xr_t b);
long xr_log2_bound(xr_t x);
xr_t xr_near_int(const xr_t x);
void xr_dotdump (const char* dotfilename, const xr_t x, const int showcache);
double xr_get_d (const xr_t x, int n);
int xr_print (const xr_t x, const int n);
int xr_print_nl (const xr_t x, const int n);
void xr_timing (int k);

DESCRIPTION

The functions in the xr family manipulate exact real numbers using the scaled-integer representation invented by Boehm et al. [1] and developed further by Ménissier-Morain [2]. They are intended for proving inequalities between quantities computed from exact (i.e. rational) data, something impossible with floating-point arithmetic. In this system a real x hat is represented internally by a function x: {Z ⁺} -> Z which satisfies (for all n>=0 and for some fixed integer B>0 )

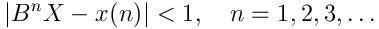The various arithmetic functions maintain this inequality through all operations.

All computations depend on the parameter b (the `granularity') which by default is 2. It can be set with xr_set_b(b) before initialization any exact reals, but should then not be changed again until the end of the computation. Values of b such as 1,3,4,5 may be faster on some problems, but all output should be the same.

FUNCTIONS

Initialization and clearing

xr_set_b(b), xr_get_b(), xr_init(n,d): Set and get the parameter b (typically 2,3,4; default if not set is 2) and initialize an exact real to the rational n/d.
xr_free(x): frees x but not the exact reals it depends on. This can lead to unreferenced and hence unreclaimable memory.

Unary arithmetic operations

xr_abs(x), xr_neg(x), xr_recip(x), xr_sqr(x), xr_sqrt(x), xr_root(x,n): Absolute value, negative, reciprocal, square, square root, n th root

Bunary arithmetic operations

(i.e. Semi-unary: first argument long, second argument xr_t)

xr_iadd(n,x), xr_isub(n,s), xr_imul(n,s): e.g. iadd adds a long to an xr_t, and will be faster than converting the long to an xr.

Ubnary arithmetic operations

(i.e. first argument xr_t, second argument long)

xr_divi(x,y), xr_powi(x,n), xr_root(x,n): Divide by integer, integer power, integer root.

Binary arithmetic operations

xr_add(x,y), xr_sub(x,y), xr_mul(x,y), xr_div(x,y): Add, subtract, multiply, divide two exact reals.

Other arithmetic operations

xr_cmp(x,y): Initiates evaluation of x and y, and terminates when it can decide that they are unequal, returning 1 for x>y and -1 for x<y. It never terminates if x=y.
xr_log2_bound(x): returns an integer k such that | x / {2 ^k} | < 1 It is safe to call with any argument.
xr_near_int(x): return either the floor or ceiling of an xr_t (this is a typical multivalued exact real function - the floor and ceiling themselves are not computable). It is safe to call with any argument.

Transcendental functions

xr_exp(x), xr_pi(void): Others are under development.

Output

xr_get_d(x,n), char* xr_get_str(x,n), xr_print(x,n), xr_print_nl(x,n): These functions try to get n correct decimals of x, but do not guarantee correctness. xr_get_d uses double-precision arithmetic internally and so is subject to exponent range limitations. These functions do not terminate if x=0.
xr_dotdump(dotfilename,x,showcache): writes a file dotfilename.dot in the graphviz [4] dot format, for conversion to a graphic represention of the internal data structure.

NOTES

The underlying large-integer arithmetic is done with the gmp library [3]. There is no floating-point arithmetic used anywhere except in the xr_get_d and pi functions. See the programs ..._test.c for examples. A simple C++ interface is defined in xr++.h It just defines one class xr and overloads the basic operators. The function names are the same, but without the xr_ prefix.

EXAMPLE C APPLICATION

/* gcc -O example.c xr.o -lm -lgmp -o example */
#include "xr.h"
int main() { /* test whether exp(pi*sqrt(163)) is integral */
  xr_t x;
  x=xr_exp(xr_mul(xr_pi(),xr_sqrt(xr_init(163,1))));
  printf("%d\n",xr_cmp(x,xr_near_int(x)));
  return 0;
}

EXAMPLE C++ APPLICATION

// g++ -O example.cc xr.o -lm -lgmp -o example
#include "xr++.h"
int main() { // test whether exp(pi*sqrt(163)) is integral
  xr x;
  x=exp(pi()*sqrt(xr(163)));
  cout<<(x>near_int(x))<<endl;
  return 0;
}

CONFORMING TO

ANSI C (I hope)

AUTHOR

Keith Briggs

HISTORY

Version 1.0 2003 March 31. I have written other implementations in python and C++. The aim of this C version is faster performance and greater ease of integration into existing code.