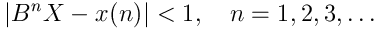xrc (exact reals in C)

This is an implementation of lazy exact real arithmetic in C. It is an alternative to multiple-precision floating-point codes. An important distinction is that in multiple-precision floating-point, one sets the precision before starting a computation, and then one cannot be sure of the final result. Interval arithmetic is an improvement on this, but still not an ideal solution because if the final interval is larger than desired, there is no simple way to restart the computation at higher precision. By constrast, in exact real arithmetic no precision level is set in advance, and no computation takes place until a final request takes place for some output. I have previously developed similar codes in python and C++. This new C version is faster, more portable, and easier to use.

usage

See the man page.

author

Keith Briggs

how does it work?

In this code, to each (mathematical) real number X in R there corresponds an xr_t x, which is a function int -> mpz_t, where mpz_t is an arbitrary precision integer type. This function is normally not called by the user. It always satisfies

where X is the real represented by x. This inequality is propagated through all operations.

B=2^b is typically 2=2¹. b can be chosen by the user (1,2,3,...), but 1 seems a good value. All results should be invariant with respect to b.

applications

The intended applications are proving inequalities between constructed reals. I initially developed this code as I had a need in my work on simultaneous Diophantine approximation algorithms. A typical situation there is that we have two irrational numbers a1,a2 and some very large integers p1,p2,q such that e1=|q*a1-p1| and e2=|q*a2-p2| are very small and very close, but we have to decide which is smaller. The result of such a computation with xrc is guaranteed correct.

A simpler well-known example is this: suppose we want to know whether exp(p*sqrt(163)) is an integer or not. In double precision, we cannot conclude anything:

double x=exp(3.141592653589793*sqrt(163));
cout << setprecision(16) << x; // prints 262537412640767947.

but in xrc we can just do this:

x=xr_exp(xr_pi()*xr_sqrt(xr_init(163,1)));
y=xr_nearint(x);
printf("%d",y!=x);

which is a proof that x is not an integer, since the output means that it is strictly greater than its floor and strictly less than its ceiling.

There are probably other applications in computational geometry, but this is NOT the right code to use if you want to look at a million decimals of p!

download

xrc-1.2.tar.gz

other attempts at similar things

Some possibly competing projects with xrc include:

CORE library (Yap)
IC-Reals: C library for Exact Real Computation (Edalat)
A Calculator for Exact Real Number Computation (Plume)
iRRAM - Exact Arithmetic in C++ (N. Müller)
MPFR
Arithmos
Exact Reals Calculator in Java (Boehm)
Computable Real Numbers in Lisp

webliography

I obtained theoretical ideas and algorithms from these sites:

H.-J. Boehm, R. Cartwright, M. Riggle, and M.J. O'Donnell. `Exact real arithmetic: A case study in higher order programming', ACM Symposium on Lisp and Functional Programming, 1986.
John Harrison: Theorem Proving with the Real Numbers and lecture notes
Valérie Ménissier-Morain: homepage
Peter Potts: Exact Real Arithmetic using Möbius Transformations
Vernon A. Lee: Optimizing Programs over the Constructive Reals
Computability and Complexity in Analysis Network
Pietro Di Gianantonio: papers on real number computability
Reinhold Heckmann: Exact Real Arithmetic
Abbas Edalat: research papers
Martín Escardó: research page and research papers
R. B. Jones: Computing with Reals - Some History
Alex Simpson: Research
Alex Kaganovsky
K. Weihrauch: Computable Analysis