An odd question

The following problem was posed by Alf van der Poorten here.

Consider the set of integers M defined by 

  (a) M contains 1
  (b) n in M entails 2n+1 in M
  (c) 3n in M implies that n is in M

Find the smallest odd integer not in M.

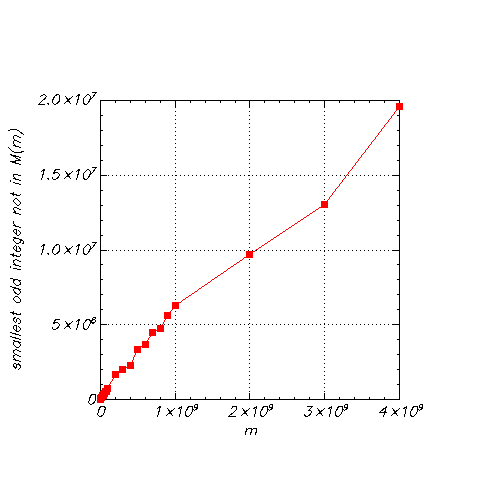
Here are the results of my own computation, which, for various values of m, solves this problem:

Consider the set of integers M(m) defined by 

  (a) max_k { k in M(m) } = m
  (b) M(m) contains 1
  (c) n in M(m) and 2n+1≤m entails 2n+1 in M(m)
  (d) 3n in M(m) implies that n is in M(m)

Find the smallest odd integer not in M(m).

1000000 8193
2000000 28673
3000000 36545
4000000 45057
5000000 55809
6000000 62977
7000000 63489
8000000 77825
9000000 98305
10000000 98305
20000000 192513
30000000 274433
40000000 282625
50000000 376833
60000000 434177
70000000 565249
80000000 565249
90000000 565249
100000000 741377
200000000 1679361
300000000 2007041
400000000 2314241
500000000 3362817
600000000 3725825
700000000 4476929
800000000 4774401
900000000 5664769
1000000000 6291457
2000000000 9699329
3000000000 13008897
4000000000 19570689